1. 勾股定理的逆定理:如果三角形的三边长分别为 $a$,$b$,$c$,且
$a^{2}+b^{2}=c^{2}$
,那么这个三角形是直角三角形。答案:$a^{2}+b^{2}=c^{2}$
2. 如果三个正整数 $a$,$b$,$c$ 满足关系
$a^{2}+b^{2}=c^{2}$
,则称 $a$,$b$,$c$ 为勾股数。答案:$a^{2}+b^{2}=c^{2}$
1. 下面四组线段中,可以构成直角三角形的是(
A.$3$,$4$,$5$
B.$4$,$5$,$6$
C.$5$,$6$,$11$
D.$2$,$3$,$4$
A
)A.$3$,$4$,$5$
B.$4$,$5$,$6$
C.$5$,$6$,$11$
D.$2$,$3$,$4$
答案:A
2. 一个三角形的三边长分别为 $0.3$,$0.4$,$0.5$,则此三角形的形状是(
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
B
)A.锐角三角形
B.直角三角形
C.钝角三角形
D.不能确定
答案:B
解析:
因为$0.3^{2} + 0.4^{2} = 0.09 + 0.16 = 0.25$,$0.5^{2} = 0.25$,所以$0.3^{2} + 0.4^{2} = 0.5^{2}$,故此三角形是直角三角形。
B
B
3. 如图,在 $\triangle ABC$ 中,$AB = 6\ cm$,$BC = 8\ cm$,$AC = 10\ cm$,若 $D$ 是 $AC$ 边的中点,则 $BD= $
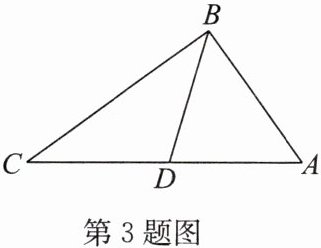
5
$cm$。
答案:5
解析:
解:在$\triangle ABC$中,$AB = 6\,cm$,$BC = 8\,cm$,$AC = 10\,cm$。
因为$AB^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100$,$AC^2 = 10^2 = 100$,所以$AB^2 + BC^2 = AC^2$,$\triangle ABC$是直角三角形,$\angle ABC = 90°$。
因为$D$是$AC$边的中点,直角三角形斜边中线等于斜边的一半,所以$BD = \frac{1}{2}AC = \frac{1}{2} × 10 = 5\,cm$。
5
因为$AB^2 + BC^2 = 6^2 + 8^2 = 36 + 64 = 100$,$AC^2 = 10^2 = 100$,所以$AB^2 + BC^2 = AC^2$,$\triangle ABC$是直角三角形,$\angle ABC = 90°$。
因为$D$是$AC$边的中点,直角三角形斜边中线等于斜边的一半,所以$BD = \frac{1}{2}AC = \frac{1}{2} × 10 = 5\,cm$。
5
4. 如图,每个方格都是边长为 $1$ 的小正方形,每个小正方形的顶点称为格点,$\triangle ABC$ 的顶点在格点上,请按要求完成下列各题。
(1)填空:$AB^{2}=$
(2)试判断 $\triangle ABC$ 的形状,并说明理由。
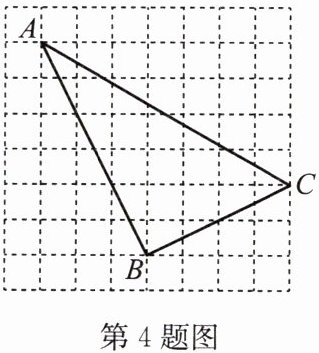
(2)解:△ABC是直角三角形.理由如下:
∵$AB^{2}=45$,$BC^{2}=20$,$AC^{2}=65$,
∴$AB^{2}+BC^{2}=AC^{2}$,
∴△ABC是直角三角形.
(1)填空:$AB^{2}=$
45
,$BC^{2}=$20
,$AC^{2}=$65
;(2)试判断 $\triangle ABC$ 的形状,并说明理由。

(2)解:△ABC是直角三角形.理由如下:
∵$AB^{2}=45$,$BC^{2}=20$,$AC^{2}=65$,
∴$AB^{2}+BC^{2}=AC^{2}$,
∴△ABC是直角三角形.
答案:
(1)45 20 65
(2)解:△ABC是直角三角形.理由如下:
∵$AB^{2}=45$,$BC^{2}=20$,$AC^{2}=65$,
∴$AB^{2}+BC^{2}=AC^{2}$,
∴△ABC是直角三角形.
(1)45 20 65
(2)解:△ABC是直角三角形.理由如下:
∵$AB^{2}=45$,$BC^{2}=20$,$AC^{2}=65$,
∴$AB^{2}+BC^{2}=AC^{2}$,
∴△ABC是直角三角形.
5. 如图,在四边形 $ABCD$ 中,$\angle ABC = 90^{\circ}$,$AB = BC = 2$,$CD = 1$,$DA = 3$。求 $\angle BCD$ 的度数。
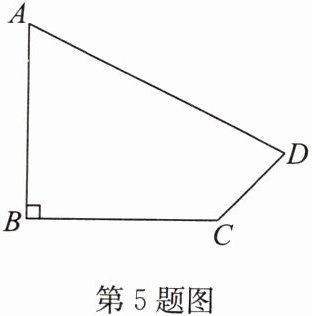

答案:解:连接AC.
∵∠ABC=90°,AB=BC=2,
∴∠ACB=45°,$AC^{2}=AB^{2}+BC^{2}=8$.
在△ACD中,
∵$AC^{2}+CD^{2}=8+1=9=DA^{2}$,
∴∠ACD=90°,
∴∠BCD=∠ACB+∠ACD=135°.
∵∠ABC=90°,AB=BC=2,
∴∠ACB=45°,$AC^{2}=AB^{2}+BC^{2}=8$.
在△ACD中,
∵$AC^{2}+CD^{2}=8+1=9=DA^{2}$,
∴∠ACD=90°,
∴∠BCD=∠ACB+∠ACD=135°.