用勾股定理及其逆定理解决实际问题的关键是构造出
直角
三角形.答案:直角
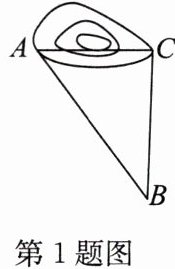
1. 如图,为修建高速铁路需凿通隧道 $AC$,测得 $\angle ACB = 90^{\circ}$,$AB = 15\ km$,$BC = 12\ km$,若每天可凿隧道 $0.3\ km$,需要几天才能将隧道 $AC$ 凿通?

答案:解:
∵∠ACB=90°,AB=15 km,BC=12 km,
∴AC²=AB²-BC²=15²-12²=81,
∴AC=9 km,9÷0.3=30(天).答:需要30天才能将隧道AC凿通.
∵∠ACB=90°,AB=15 km,BC=12 km,
∴AC²=AB²-BC²=15²-12²=81,
∴AC=9 km,9÷0.3=30(天).答:需要30天才能将隧道AC凿通.
2. 有一道“折竹”问题:“今有竹高一丈,末折抵地,去本四尺. 问:折者高几何?”题意是:一根竹子原高 $1$ 丈,中部有一处折断,竹梢触地面处离竹根 $4$ 尺,试问折断处离地面多高?($1$ 丈 $= 10$ 尺)
答案:解:设折断处离地面x尺,根据题意,得x²+4²=(10-x)²,解得x=4.2.答:折断处离地面4.2尺.
3. 如图,在平静的湖面上,有一支红莲 $BA$,高出水面的部分 $AC$ 为 $1$ 米,一阵风吹来,红莲被吹到一边,花朵齐及水面(即 $AB = DB$),已知红莲移动的水平距离 $CD$ 为 $3$ 米,则湖水深 $BC$ 为多少米?
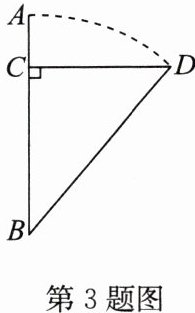

答案:解:设BC为h米,则AB=BD=(h+1)米.由勾股定理得BD²=DC²+BC²,即(h+1)²=3²+h²,解得h=4.因此湖水深BC为4米.
解析:
解:设$BC$为$h$米,则$AB = BD=(h + 1)$米。
由勾股定理得$BD^{2}=DC^{2}+BC^{2}$,即$(h + 1)^{2}=3^{2}+h^{2}$。
展开得$h^{2}+2h + 1=9 + h^{2}$,
移项化简得$2h=8$,解得$h = 4$。
因此湖水深$BC$为$4$米。
由勾股定理得$BD^{2}=DC^{2}+BC^{2}$,即$(h + 1)^{2}=3^{2}+h^{2}$。
展开得$h^{2}+2h + 1=9 + h^{2}$,
移项化简得$2h=8$,解得$h = 4$。
因此湖水深$BC$为$4$米。