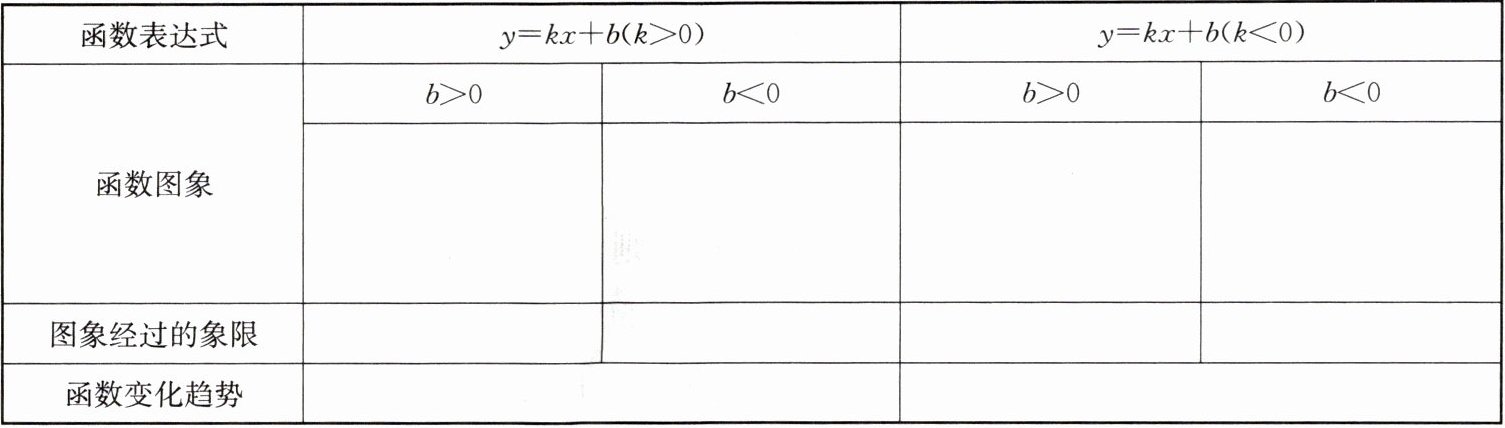
一次函数 $ y = kx + b $($ k $,$ b $ 为常数,$ k \neq 0 $)的图象特征和性质:

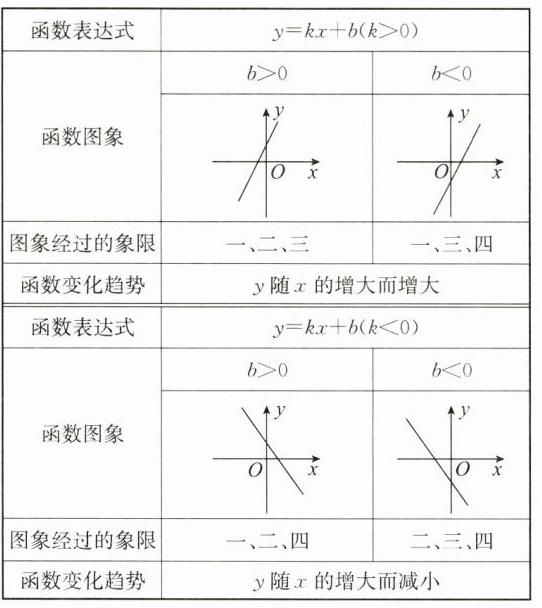
答案:

1. 一次函数 $ y = 3x - 4 $ 的图象经过 (
A.第一、二、三象限
B.第二、三、四象限
C.第一、三、四象限
D.第一、二、四象限
C
)A.第一、二、三象限
B.第二、三、四象限
C.第一、三、四象限
D.第一、二、四象限
答案:C
解析:
对于一次函数$y = kx + b$($k$,$b$为常数,$k \neq 0$):
当$k > 0$时,函数图象从左到右上升,经过第一、三象限;
当$k < 0$时,函数图象从左到右下降,经过第二、四象限;
当$b > 0$时,函数图象与$y$轴交于正半轴;
当$b < 0$时,函数图象与$y$轴交于负半轴。
在一次函数$y = 3x - 4$中,$k = 3 > 0$,$b = - 4 < 0$,所以函数图象经过第一、三象限,且与$y$轴交于负半轴,即经过第四象限。综上,该函数图象经过第一、三、四象限。
C
当$k > 0$时,函数图象从左到右上升,经过第一、三象限;
当$k < 0$时,函数图象从左到右下降,经过第二、四象限;
当$b > 0$时,函数图象与$y$轴交于正半轴;
当$b < 0$时,函数图象与$y$轴交于负半轴。
在一次函数$y = 3x - 4$中,$k = 3 > 0$,$b = - 4 < 0$,所以函数图象经过第一、三象限,且与$y$轴交于负半轴,即经过第四象限。综上,该函数图象经过第一、三、四象限。
C
2. 已知一次函数 $ y = (m - 3)x + 5 $,$ y $ 随 $ x $ 的增大而增大,那么 $ m $ 的取值范围是 (
A.$ m < 3 $
B.$ m > 3 $
C.$ m < - 3 $
D.$ m > - 3 $
B
)A.$ m < 3 $
B.$ m > 3 $
C.$ m < - 3 $
D.$ m > - 3 $
答案:B
解析:
对于一次函数$y=(m - 3)x + 5$,当$y$随$x$的增大而增大时,其斜率$m - 3>0$,解得$m>3$。
B
B
3. 已知一次函数 $ y = 2x - 1 $ 的图象经过点 $ A(a,3) $,$ B(b,-1) $,$ C(c,5) $,则 $ a $,$ b $,$ c $ 的大小关系是 (
A.$ a < b < c $
B.$ b < c < a $
C.$ c < a < b $
D.$ b < a < c $
D
)A.$ a < b < c $
B.$ b < c < a $
C.$ c < a < b $
D.$ b < a < c $
答案:D
解析:
将点$A(a,3)$代入$y = 2x - 1$,得$3 = 2a - 1$,解得$a = 2$;
将点$B(b,-1)$代入$y = 2x - 1$,得$-1 = 2b - 1$,解得$b = 0$;
将点$C(c,5)$代入$y = 2x - 1$,得$5 = 2c - 1$,解得$c = 3$;
因为$0 < 2 < 3$,所以$b < a < c$。
D
将点$B(b,-1)$代入$y = 2x - 1$,得$-1 = 2b - 1$,解得$b = 0$;
将点$C(c,5)$代入$y = 2x - 1$,得$5 = 2c - 1$,解得$c = 3$;
因为$0 < 2 < 3$,所以$b < a < c$。
D
4. 已知函数 $ y = (m - 4)x + 2m - 5 $,当 $ m $ 的取值范围为
$\frac{5}{2}$<m<4
时,其图象经过第一、二、四象限.答案:$\frac{5}{2}$<m<4
解析:
要使函数$y=(m - 4)x + 2m - 5$的图象经过第一、二、四象限,需满足:
斜率小于$0$:$m - 4 < 0$,解得$m < 4$;
截距大于$0$:$2m - 5 > 0$,解得$m > \frac{5}{2}$。
综上,$m$的取值范围为$\frac{5}{2} < m < 4$。
$\frac{5}{2} < m < 4$
斜率小于$0$:$m - 4 < 0$,解得$m < 4$;
截距大于$0$:$2m - 5 > 0$,解得$m > \frac{5}{2}$。
综上,$m$的取值范围为$\frac{5}{2} < m < 4$。
$\frac{5}{2} < m < 4$
5. 若直线 $ y = 2x + 1 $ 向下平移后经过点 $ (5,1) $,则平移后的直线的函数表达式为
y=2x−9
.答案:y=2x−9
解析:
设平移后的直线函数表达式为$y = 2x + b$。
因为平移后的直线经过点$(5,1)$,将$x = 5$,$y = 1$代入表达式得:$1 = 2×5 + b$,即$1 = 10 + b$,解得$b = -9$。
所以平移后的直线的函数表达式为$y = 2x - 9$。
因为平移后的直线经过点$(5,1)$,将$x = 5$,$y = 1$代入表达式得:$1 = 2×5 + b$,即$1 = 10 + b$,解得$b = -9$。
所以平移后的直线的函数表达式为$y = 2x - 9$。
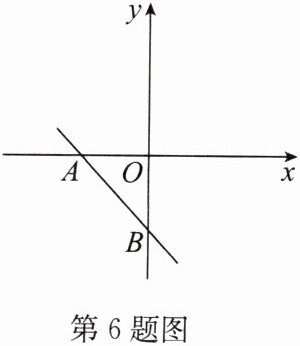
6. 如图,一次函数 $ y = (m - 3)x - m + 1 $ 的图象分别与 $ x $ 轴的负半轴和 $ y $ 轴的负半轴相交于点 $ A $,$ B $.
(1) 求 $ m $ 的取值范围;
(2) 若该一次函数的图象向上平移 $ 3 $ 个单位长度就经过原点,求 $ m $ 的值.
(1) 求 $ m $ 的取值范围;
(2) 若该一次函数的图象向上平移 $ 3 $ 个单位长度就经过原点,求 $ m $ 的值.

答案:解:
(1)
∵该函数的图象经过第二、三、四象限,
∴m−3<0,且−m+1<0,解得1<m<3.
(2)该一次函数的图象向上平移3个单位长度得到的图象对应的函数表达式为y=(m−3)x−m+1+3=(m−3)x−m+4.
∵平移后的函数图象经过原点,
∴把(0,0)代入y=(m−3)x−m+4,得−m+4=0,解得m=4.
(1)
∵该函数的图象经过第二、三、四象限,
∴m−3<0,且−m+1<0,解得1<m<3.
(2)该一次函数的图象向上平移3个单位长度得到的图象对应的函数表达式为y=(m−3)x−m+1+3=(m−3)x−m+4.
∵平移后的函数图象经过原点,
∴把(0,0)代入y=(m−3)x−m+4,得−m+4=0,解得m=4.