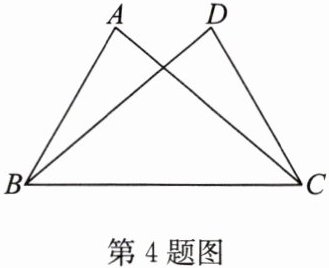
4. 如图,△ABC≌△DCB,若∠A = 80°,∠DBC = 40°,则∠DCA的度数为
20°
。
答案:20°
解析:
证明:
∵△ABC≌△DCB,
∴∠A=∠D=80°,∠ABC=∠DCB,AB=DC,BC=CB。
在△ABC中,∠ABC+∠A+∠ACB=180°,
又
∵∠DBC=40°,设∠ACB=∠DBC+∠DCA=40°+∠DCA,∠ABC=∠DCB=∠ACB,
∴∠ABC=40°+∠DCA。
∴(40°+∠DCA)+80°+(40°+∠DCA)=180°,
解得∠DCA=20°。
20°
∵△ABC≌△DCB,
∴∠A=∠D=80°,∠ABC=∠DCB,AB=DC,BC=CB。
在△ABC中,∠ABC+∠A+∠ACB=180°,
又
∵∠DBC=40°,设∠ACB=∠DBC+∠DCA=40°+∠DCA,∠ABC=∠DCB=∠ACB,
∴∠ABC=40°+∠DCA。
∴(40°+∠DCA)+80°+(40°+∠DCA)=180°,
解得∠DCA=20°。
20°
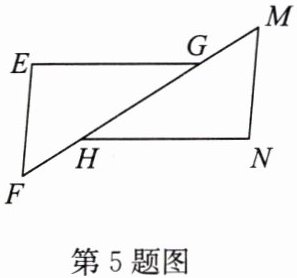
5. 如图,已知△EFG≌△NMH,∠F与∠M是对应角。
(1)求证:FH = GM;
(2)若FH = 1.1 cm,HM = 3.3 cm,求HG的长度。
(1)求证:FH = GM;
(2)若FH = 1.1 cm,HM = 3.3 cm,求HG的长度。

答案:
(1)证明:
∵△EFG≌△NMH,∠F与∠M是对应角,
∴FG=MH,
∴FG-HG=MH-HG,即 FH=GM.
(2)解:
∵△EFG≌△NMH,
∴FG=HM=3.3 cm.
∴HG=FG-FH=3.3-1.1=2.2(cm).
(1)证明:
∵△EFG≌△NMH,∠F与∠M是对应角,
∴FG=MH,
∴FG-HG=MH-HG,即 FH=GM.
(2)解:
∵△EFG≌△NMH,
∴FG=HM=3.3 cm.
∴HG=FG-FH=3.3-1.1=2.2(cm).