例 1 某船往返于 A、B 两码头之间,顺流时速度为 $ v_1 $,逆流时速度为 $ v_2 $,求该船在 A、B 两码头之间往返一次的平均速度。
答案:设A、B两码头之间的距离为$s$。
1. 往返总路程:$s_{总} = s + s = 2s$。
2. 顺流时间:$t_1 = \frac{s}{v_1}$;逆流时间:$t_2 = \frac{s}{v_2}$。
3. 往返总时间:$t_{总} = t_1 + t_2 = \frac{s}{v_1} + \frac{s}{v_2} = s\left(\frac{1}{v_1} + \frac{1}{v_2}\right) = s\cdot\frac{v_1 + v_2}{v_1v_2}$。
4. 平均速度:$v_{平均} = \frac{s_{总}}{t_{总}} = \frac{2s}{s\cdot\frac{v_1 + v_2}{v_1v_2}} = \frac{2v_1v_2}{v_1 + v_2}$。
结论:该船往返一次的平均速度为$\frac{2v_1v_2}{v_1 + v_2}$。
1. 往返总路程:$s_{总} = s + s = 2s$。
2. 顺流时间:$t_1 = \frac{s}{v_1}$;逆流时间:$t_2 = \frac{s}{v_2}$。
3. 往返总时间:$t_{总} = t_1 + t_2 = \frac{s}{v_1} + \frac{s}{v_2} = s\left(\frac{1}{v_1} + \frac{1}{v_2}\right) = s\cdot\frac{v_1 + v_2}{v_1v_2}$。
4. 平均速度:$v_{平均} = \frac{s_{总}}{t_{总}} = \frac{2s}{s\cdot\frac{v_1 + v_2}{v_1v_2}} = \frac{2v_1v_2}{v_1 + v_2}$。
结论:该船往返一次的平均速度为$\frac{2v_1v_2}{v_1 + v_2}$。
例 2 用图像可以表示物体的运动规律,下图中可以表示物体做匀速直线运动的是(
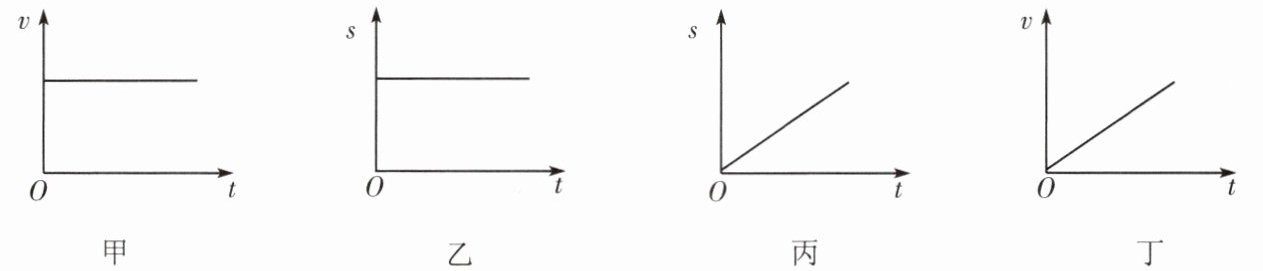
A.乙、丁
B.甲、丙
C.甲、丁
D.乙、丙
B
)
A.乙、丁
B.甲、丙
C.甲、丁
D.乙、丙
答案:B
例 3 A、B 两列车的运行时刻见下表。
|列车|运行时间|运动距离/km|
|A 列车(甲地—乙地)|8:34 开 13:49 到|840|
|B 列车(乙地—甲地)|15:31 开 20:39 到|840|

根据上述列车运行时刻表的信息可知:A 列车从甲地到乙地所用的时间是
|列车|运行时间|运动距离/km|
|A 列车(甲地—乙地)|8:34 开 13:49 到|840|
|B 列车(乙地—甲地)|15:31 开 20:39 到|840|

根据上述列车运行时刻表的信息可知:A 列车从甲地到乙地所用的时间是
315
min,它的平均速度为160
km/h。B 列车的平均速度比 A 列车的大
。答案:315
160
大
160
大
例 4 汽车追尾是高速公路上经常发生的一类交通事故,其重要原因是遇到意外情况时汽车不能立即停下。研究发现,司机从看到危险情况到踩刹车需要一段时间,这段时间叫作反应时间。在反应时间内汽车要保持原来速度前进一段距离,这段距离叫作反应距离;从踩刹车到汽车停止,汽车还要减速前进一段距离,这段距离叫作制动距离,如图所示。

下表是一个机警的司机驾驶一辆保养得很好的汽车,在干燥的水平公路上以不同的速度行驶时测得的反应距离和制动距离。
|行驶速度 $ v/(km \cdot h^{-1}) $|反应距离 $ s_1/m $|制动距离 $ s_2/m $|
|60|11|20|
|80|15|34|
|100|19|54|

(1)利用表中的数据算出该司机的反应时间为______ s。(保留两位小数)

(2)由这个测试可知,______是影响汽车制动距离的主要因素。
(3)请在右图中画出从司机看到危险情况开始计时,到汽车停止的这段时间内,汽车运动的 $ v-t $ 图像。(不需要准确描点)

下表是一个机警的司机驾驶一辆保养得很好的汽车,在干燥的水平公路上以不同的速度行驶时测得的反应距离和制动距离。
|行驶速度 $ v/(km \cdot h^{-1}) $|反应距离 $ s_1/m $|制动距离 $ s_2/m $|
|60|11|20|
|80|15|34|
|100|19|54|

(1)利用表中的数据算出该司机的反应时间为______ s。(保留两位小数)

(2)由这个测试可知,______是影响汽车制动距离的主要因素。
(3)请在右图中画出从司机看到危险情况开始计时,到汽车停止的这段时间内,汽车运动的 $ v-t $ 图像。(不需要准确描点)
答案:
0.67
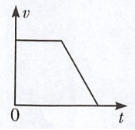
车速
0.67

车速