1. 电功率是描述
2. 电功率的计算公式是$P = \frac{W}{t} =$
3. 电功率的国际单位是
4. 用$W = Pt$计算电功时,若功率的单位是
电流做功快慢
的物理量。2. 电功率的计算公式是$P = \frac{W}{t} =$
UI
,这个公式适用于任何电路(或“用电器”)。根据欧姆定律可推出$P =$$\frac{U^{2}}{R}$
和$P =$$I^{2}R$
,这两个公式只适用于纯电阻电路。3. 电功率的国际单位是
瓦(W)
。$1 \ kW =$$10^{3}$
$\ W$,$1\ mW =$$10^{-3}$
$\ W$。4. 用$W = Pt$计算电功时,若功率的单位是
千瓦(kW)
,时间的单位是小时(h)
,则电功的单位是千瓦时($kW · h$)。答案:1.电流做功快慢$ 2.UI \frac{U^{2}}{R} I^{2}R 3.$瓦$(W) 10^{3} 10^{-3} 4.$千瓦(kW) 小时(h)
1. 做同样多的功,电功率大的用电器花的时间
少
;在相同的时间里,电功率大的用电器做的功多
。(多/少)答案:1.少 多
2. 小明让家中某用电器单独工作$0.5\ h$,观察到家中电能表的示数由$\boxed{00027.62}$变为$\boxed{00028.22}$,则该用电器消耗的电能是
0.6
$\ kW · h$,该用电器的电功率是1.2
$\ kW$。答案:2.0.6 1.2
3. 某小灯泡两端的电压为$2.5\ V$,通过的电流为$0.3\ A$,则小灯泡的电功率为
0.75
$\ W$,此小灯泡在$5\ min$内消耗的电能是225
$\ J$。答案:3.0.75 225
解析:
解:已知小灯泡两端电压$U = 2.5\ V$,通过电流$I = 0.3\ A$。
电功率$P = UI = 2.5\ V×0.3\ A = 0.75\ W$。
时间$t = 5\ min = 5×60\ s = 300\ s$,消耗电能$W = Pt = 0.75\ W×300\ s = 225\ J$。
0.75;225
电功率$P = UI = 2.5\ V×0.3\ A = 0.75\ W$。
时间$t = 5\ min = 5×60\ s = 300\ s$,消耗电能$W = Pt = 0.75\ W×300\ s = 225\ J$。
0.75;225
4. 如果加在定值电阻两端的电压从$8\ V$增加到$10\ V$时,通过定值电阻的电流相应变化了$0.2\ A$,那么该定值电阻的阻值是
10
$\ \Omega$,所消耗的电功率的变化量是3.6
$\ W$。答案:4.10 3.6
解析:
解:设该定值电阻的阻值为$R$。
当电压$U_1 = 8\ V$时,电流$I_1=\frac{U_1}{R}=\frac{8}{R}$;当电压$U_2 = 10\ V$时,电流$I_2=\frac{U_2}{R}=\frac{10}{R}$。
电流变化量$\Delta I = I_2 - I_1 = 0.2\ A$,即$\frac{10}{R}-\frac{8}{R}=0.2$,解得$R = 10\ \Omega$。
电压为$8\ V$时,电功率$P_1=\frac{U_1^2}{R}=\frac{8^2}{10}=6.4\ W$;电压为$10\ V$时,电功率$P_2=\frac{U_2^2}{R}=\frac{10^2}{10}=10\ W$。
电功率变化量$\Delta P = P_2 - P_1=10 - 6.4 = 3.6\ W$。
10;3.6
当电压$U_1 = 8\ V$时,电流$I_1=\frac{U_1}{R}=\frac{8}{R}$;当电压$U_2 = 10\ V$时,电流$I_2=\frac{U_2}{R}=\frac{10}{R}$。
电流变化量$\Delta I = I_2 - I_1 = 0.2\ A$,即$\frac{10}{R}-\frac{8}{R}=0.2$,解得$R = 10\ \Omega$。
电压为$8\ V$时,电功率$P_1=\frac{U_1^2}{R}=\frac{8^2}{10}=6.4\ W$;电压为$10\ V$时,电功率$P_2=\frac{U_2^2}{R}=\frac{10^2}{10}=10\ W$。
电功率变化量$\Delta P = P_2 - P_1=10 - 6.4 = 3.6\ W$。
10;3.6
5. 某灯泡接在$220\ V$的电路中时,消耗的电功率是$40\ W$,则:
(1) 通过灯丝的电流约是
(2) 灯丝的电阻是
(3) 工作$10\ min$,灯泡消耗的电能是
(1) 通过灯丝的电流约是
0.18
$\ A$。(结果保留两位小数)(2) 灯丝的电阻是
1210
$\ \Omega$。(3) 工作$10\ min$,灯泡消耗的电能是
$2.4×10^{4}$
$\ J$。答案:$5.(1)0.18 (2)1210 (3)2.4×10^{4}$
解析:
(1)已知灯泡两端电压$U = 220\ V$,电功率$P = 40\ W$,根据公式$P=UI$,可得电流$I=\frac{P}{U}=\frac{40\ W}{220\ V}\approx0.18\ A$。
(2)由$P = \frac{U^{2}}{R}$可得,灯丝电阻$R=\frac{U^{2}}{P}=\frac{(220\ V)^{2}}{40\ W}=\frac{48400\ V^{2}}{40\ W} = 1210\ \Omega$。
(3)工作时间$t=10\ min=10×60\ s = 600\ s$,根据$W = Pt$,消耗电能$W=40\ W×600\ s=24000\ J=2.4×10^{4}\ J$。
(2)由$P = \frac{U^{2}}{R}$可得,灯丝电阻$R=\frac{U^{2}}{P}=\frac{(220\ V)^{2}}{40\ W}=\frac{48400\ V^{2}}{40\ W} = 1210\ \Omega$。
(3)工作时间$t=10\ min=10×60\ s = 600\ s$,根据$W = Pt$,消耗电能$W=40\ W×600\ s=24000\ J=2.4×10^{4}\ J$。
6. 在如图所示的电路中,电源电压保持$6\ V$不变,电阻$R_1$的阻值为$20\ \Omega$。当开关$S_2$断开,$S_1$、$S_3$闭合时,电流表的示数为$0.45\ A$。求:
(1) 当开关$S_2$断开,$S_1$、$S_3$闭合时,电阻$R_2$消耗的电功率。
(2) 当开关$S_1$、$S_3$断开,$S_2$闭合时,电路消耗的总电功率。
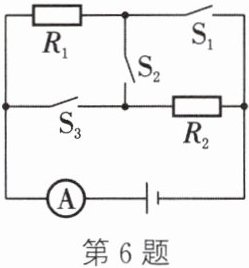
(1) 当开关$S_2$断开,$S_1$、$S_3$闭合时,电阻$R_2$消耗的电功率。
(2) 当开关$S_1$、$S_3$断开,$S_2$闭合时,电路消耗的总电功率。

答案:6.(1)$I_{1}=\frac{U}{R_{1}}=\frac{6V}{20\Omega}=0.3A$;$I_{2}=I - I_{1}=0.45A - 0.3A=0.15A$;$P = UI_{2}=6V×0.15A=0.9W$ (2)$R_{2}=\frac{U}{I_{2}}=\frac{6V}{0.15A}=40\Omega$;$R_{总}=R_{1}+R_{2}=20\Omega+40\Omega=60\Omega$;$P_{总}=\frac{U^{2}}{R_{总}}=\frac{(6V)^{2}}{60\Omega}=0.6W$
解析:
(1)解:当开关$S_2$断开,$S_1$、$S_3$闭合时,$R_1$与$R_2$并联,电流表测干路电流。
通过$R_1$的电流:$I_{1}=\frac{U}{R_{1}}=\frac{6\ V}{20\ \Omega}=0.3\ A$
通过$R_2$的电流:$I_{2}=I - I_{1}=0.45\ A-0.3\ A=0.15\ A$
$R_2$消耗的电功率:$P = UI_{2}=6\ V×0.15\ A=0.9\ W$
(2)解:$R_2$的阻值:$R_{2}=\frac{U}{I_{2}}=\frac{6\ V}{0.15\ A}=40\ \Omega$
当开关$S_1$、$S_3$断开,$S_2$闭合时,$R_1$与$R_2$串联。
总电阻:$R_{ 总}=R_{1}+R_{2}=20\ \Omega + 40\ \Omega=60\ \Omega$
电路消耗的总电功率:$P_{ 总}=\frac{U^{2}}{R_{ 总}}=\frac{(6\ V)^{2}}{60\ \Omega}=0.6\ W$
通过$R_1$的电流:$I_{1}=\frac{U}{R_{1}}=\frac{6\ V}{20\ \Omega}=0.3\ A$
通过$R_2$的电流:$I_{2}=I - I_{1}=0.45\ A-0.3\ A=0.15\ A$
$R_2$消耗的电功率:$P = UI_{2}=6\ V×0.15\ A=0.9\ W$
(2)解:$R_2$的阻值:$R_{2}=\frac{U}{I_{2}}=\frac{6\ V}{0.15\ A}=40\ \Omega$
当开关$S_1$、$S_3$断开,$S_2$闭合时,$R_1$与$R_2$串联。
总电阻:$R_{ 总}=R_{1}+R_{2}=20\ \Omega + 40\ \Omega=60\ \Omega$
电路消耗的总电功率:$P_{ 总}=\frac{U^{2}}{R_{ 总}}=\frac{(6\ V)^{2}}{60\ \Omega}=0.6\ W$