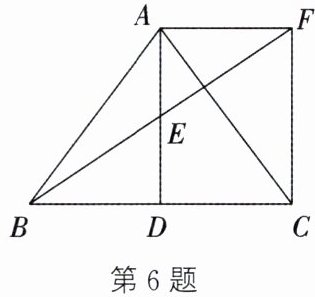
6. 如图,在 $\triangle ABC$ 中,$AB = AC$,$AD$ 为边 $BC$ 上的中线,$E$ 为 $AD$ 的中点,过点 $A$ 作 $AF // BC$,交
$BE$ 的延长线于点 $F$,连接 $CF$.
(1) 求证:四边形 $ADCF$ 为矩形;
(2) 若 $BC = 6$,$\sin \angle BAD=\frac{3}{5}$,求 $EF$ 的长.
$BE$ 的延长线于点 $F$,连接 $CF$.
(1) 求证:四边形 $ADCF$ 为矩形;
(2) 若 $BC = 6$,$\sin \angle BAD=\frac{3}{5}$,求 $EF$ 的长.

答案:6. (1)$\because AD$为边BC上的中线,$\therefore BD = CD$. $\because E$为AD的中点,$\therefore AE = ED$. $\because AF // BC$,$\therefore \angle AFE = \angle DBE$,$\angle FAE = \angle BDE$. 在$\triangle AFE$和$\triangle DBE$中,$\begin{cases} \angle AFE = \angle DBE, \\ \angle FAE = \angle BDE, \\ AE = DE, \end{cases}$ $\therefore \triangle AFE \cong \triangle DBE$. $\therefore AF = DB$. $\therefore AF = CD$.又$\because AF // BC$,$\therefore$四边形ADCF为平行四边形. $\because AB = AC$,AD为边BC上的中线,$\therefore AD \perp BC$. $\therefore \angle ADC = 90°$. $\therefore$四边形ADCF为矩形
(2)$\because BC = 6$,AD为边BC上的中线,$\therefore BD = \frac{1}{2}BC = 3$.在$Rt\triangle ABD$中,$\because \sin\angle BAD = \frac{BD}{AB} = \frac{3}{5}$,$\therefore AB = \frac{BD}{\sin\angle BAD} = 5$. $\therefore AD = \sqrt{AB^{2} - BD^{2}} = \sqrt{5^{2} - 3^{2}} = 4$.又$\because E$为AD的中点,$\therefore ED = \frac{1}{2}AD = 2$. $\therefore$在$Rt\triangle DBE$中,$BE = \sqrt{ED^{2} + BD^{2}} = \sqrt{2^{2} + 3^{2}} = \sqrt{13}$.由(1)知,$\triangle AFE \cong \triangle DBE$,$\therefore EF = BE = \sqrt{13}$
(2)$\because BC = 6$,AD为边BC上的中线,$\therefore BD = \frac{1}{2}BC = 3$.在$Rt\triangle ABD$中,$\because \sin\angle BAD = \frac{BD}{AB} = \frac{3}{5}$,$\therefore AB = \frac{BD}{\sin\angle BAD} = 5$. $\therefore AD = \sqrt{AB^{2} - BD^{2}} = \sqrt{5^{2} - 3^{2}} = 4$.又$\because E$为AD的中点,$\therefore ED = \frac{1}{2}AD = 2$. $\therefore$在$Rt\triangle DBE$中,$BE = \sqrt{ED^{2} + BD^{2}} = \sqrt{2^{2} + 3^{2}} = \sqrt{13}$.由(1)知,$\triangle AFE \cong \triangle DBE$,$\therefore EF = BE = \sqrt{13}$
7. 如图,$AB$ 是 $\odot O$ 的直径,且经过弦 $CD$ 的中点 $H$,已知 $\cos \angle CDB=\frac{4}{5}$,$BD = 5$,则 $OH$ 的长为
(

A.$\frac{7}{6}$
B.1
C.$\frac{5}{6}$
D.$\frac{2}{3}$
(
A
)
A.$\frac{7}{6}$
B.1
C.$\frac{5}{6}$
D.$\frac{2}{3}$
答案:7. A
解析:
证明:
∵AB是⊙O的直径且过CD中点H,
∴AB⊥CD,CH=DH(垂径定理)。
在Rt△BHD中,$\cos\angle CDB=\frac{DH}{BD}=\frac{4}{5}$,BD=5,
∴$DH=BD·\cos\angle CDB=5×\frac{4}{5}=4$,
由勾股定理得$BH=\sqrt{BD^2-DH^2}=\sqrt{5^2-4^2}=3$。
设OH=x,⊙O半径为r,则OB=r,BH=OB+OH=r+x=3(H在OB上),即$r=3-x$。
连接OD,则OD=r,在Rt△OHD中,$OH^2+DH^2=OD^2$,
即$x^2+4^2=(3-x)^2$,
解得$x=\frac{7}{6}$。
∴OH的长为$\frac{7}{6}$。
答案:A
∵AB是⊙O的直径且过CD中点H,
∴AB⊥CD,CH=DH(垂径定理)。
在Rt△BHD中,$\cos\angle CDB=\frac{DH}{BD}=\frac{4}{5}$,BD=5,
∴$DH=BD·\cos\angle CDB=5×\frac{4}{5}=4$,
由勾股定理得$BH=\sqrt{BD^2-DH^2}=\sqrt{5^2-4^2}=3$。
设OH=x,⊙O半径为r,则OB=r,BH=OB+OH=r+x=3(H在OB上),即$r=3-x$。
连接OD,则OD=r,在Rt△OHD中,$OH^2+DH^2=OD^2$,
即$x^2+4^2=(3-x)^2$,
解得$x=\frac{7}{6}$。
∴OH的长为$\frac{7}{6}$。
答案:A
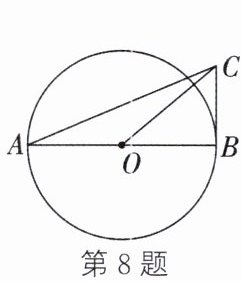
8. 如图,$AB$ 是 $\odot O$ 的直径,$BC$ 与 $\odot O$ 相切于点 $B$,连接 $AC$,$OC$. 若 $\sin \angle BAC=\frac{1}{3}$,则
$\tan \angle BOC =$
$\tan \angle BOC =$
$\frac{\sqrt{2}}{2}$
.
答案:8. $\frac{\sqrt{2}}{2}$
解析:
证明:设 $ \odot O $ 的半径为 $ r $,则 $ OA = OB = r $,$ AB = 2r $。
因为 $ BC $ 与 $ \odot O $ 相切于点 $ B $,所以 $ AB \perp BC $,即 $ \angle ABC = 90° $。
在 $ Rt\triangle ABC $ 中,$ \sin \angle BAC = \frac{BC}{AC} = \frac{1}{3} $,设 $ BC = x $,则 $ AC = 3x $。
由勾股定理得:$ AB^2 + BC^2 = AC^2 $,即 $ (2r)^2 + x^2 = (3x)^2 $,化简得 $ 4r^2 = 8x^2 $,解得 $ r = \sqrt{2}x $。
在 $ Rt\triangle OBC $ 中,$ OB = r = \sqrt{2}x $,$ BC = x $,所以 $ \tan \angle BOC = \frac{BC}{OB} = \frac{x}{\sqrt{2}x} = \frac{\sqrt{2}}{2} $。
$\frac{\sqrt{2}}{2}$
因为 $ BC $ 与 $ \odot O $ 相切于点 $ B $,所以 $ AB \perp BC $,即 $ \angle ABC = 90° $。
在 $ Rt\triangle ABC $ 中,$ \sin \angle BAC = \frac{BC}{AC} = \frac{1}{3} $,设 $ BC = x $,则 $ AC = 3x $。
由勾股定理得:$ AB^2 + BC^2 = AC^2 $,即 $ (2r)^2 + x^2 = (3x)^2 $,化简得 $ 4r^2 = 8x^2 $,解得 $ r = \sqrt{2}x $。
在 $ Rt\triangle OBC $ 中,$ OB = r = \sqrt{2}x $,$ BC = x $,所以 $ \tan \angle BOC = \frac{BC}{OB} = \frac{x}{\sqrt{2}x} = \frac{\sqrt{2}}{2} $。
$\frac{\sqrt{2}}{2}$
9. 如图,$\odot O$ 的半径为 $5$,$\triangle ABC$ 内接于 $\odot O$,$BC = 6$,$CD \perp AB$ 于点 $D$,则 $\tan \angle ACD$ 的值为
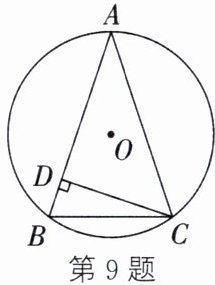
$\frac{4}{3}$
.
答案:9. $\frac{4}{3}$
解析:
证明:连接 $BO$ 并延长交 $\odot O$ 于点 $E$,连接 $CE$。
$\because BE$ 是 $\odot O$ 的直径,
$\therefore \angle BCE = 90°$,$BE = 2 × 5 = 10$。
在 $Rt\triangle BCE$ 中,$BC = 6$,
$\therefore CE = \sqrt{BE^2 - BC^2} = \sqrt{10^2 - 6^2} = 8$。
$\because \angle A = \angle E$(同弧所对的圆周角相等),
$CD \perp AB$,$\angle BCE = 90°$,
$\therefore \angle ADC = \angle BCE = 90°$,
$\therefore \angle ACD = \angle EBC$(等角的余角相等)。
在 $Rt\triangle BCE$ 中,
$\tan \angle EBC = \frac{CE}{BC} = \frac{8}{6} = \frac{4}{3}$,
$\therefore \tan \angle ACD = \frac{4}{3}$。
$\frac{4}{3}$
$\because BE$ 是 $\odot O$ 的直径,
$\therefore \angle BCE = 90°$,$BE = 2 × 5 = 10$。
在 $Rt\triangle BCE$ 中,$BC = 6$,
$\therefore CE = \sqrt{BE^2 - BC^2} = \sqrt{10^2 - 6^2} = 8$。
$\because \angle A = \angle E$(同弧所对的圆周角相等),
$CD \perp AB$,$\angle BCE = 90°$,
$\therefore \angle ADC = \angle BCE = 90°$,
$\therefore \angle ACD = \angle EBC$(等角的余角相等)。
在 $Rt\triangle BCE$ 中,
$\tan \angle EBC = \frac{CE}{BC} = \frac{8}{6} = \frac{4}{3}$,
$\therefore \tan \angle ACD = \frac{4}{3}$。
$\frac{4}{3}$
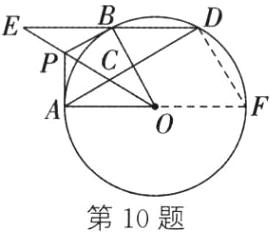
10. (2025·北京) 如图,过点 $P$ 作 $\odot O$ 的两条切线,切点分别为 $A$,$B$,连接 $OA$,$OB$,$OP$,取 $OP$ 的
中点 $C$,连接 $AC$ 并交 $\odot O$ 于点 $D$,连接 $BD$.
(1) 求证:$\angle ADB = \angle AOP$.
(2) 延长 $OP$ 交 $DB$ 的延长线于点 $E$. 若 $AP = 10$,$\tan \angle AOP=\frac{1}{2}$,求 $DE$ 的长.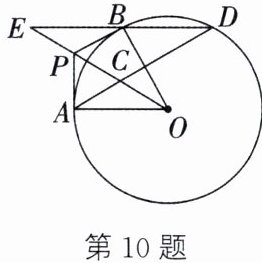
中点 $C$,连接 $AC$ 并交 $\odot O$ 于点 $D$,连接 $BD$.
(1) 求证:$\angle ADB = \angle AOP$.
(2) 延长 $OP$ 交 $DB$ 的延长线于点 $E$. 若 $AP = 10$,$\tan \angle AOP=\frac{1}{2}$,求 $DE$ 的长.

答案:
10. (1)$\because AP$,BP分别切$\odot O$于点A,B,$\therefore OP$平分$\angle AOB$. $\therefore \angle AOP = \frac{1}{2}\angle AOB$.又$\because \overset{\frown}{AB} = \overset{\frown}{AB}$,$\therefore \angle ADB = \frac{1}{2}\angle AOB$. $\therefore \angle ADB = \angle AOP$ (2)如图,延长AO交$\odot O$于点F,连接DF,则$\angle ADF = 90°$. $\because AP$,BP分别切$\odot O$于点A,B,$\therefore PA \perp OA$. $\because C$为OP的中点,$\therefore PC = OC = AC = \frac{1}{2}OP$.又$\because AP = 10$,$\tan\angle AOP = \frac{1}{2}$,$\therefore AO = \frac{AP}{\tan\angle AOP} = 20$. $\therefore OP = \sqrt{AO^{2} + AP^{2}} = \sqrt{20^{2} + 10^{2}} = 10\sqrt{5}$. $\therefore AC = OC = \frac{1}{2}OP = 5\sqrt{5}$,$AF = 2AO = 40$. $\because AC = OC$,$\therefore \angle CAO = \angle AOC$.又$\because \angle PAO = \angle ADF = 90°$,$\cos\angle DAF = \frac{DA}{FA}$,$\cos\angle POA = \frac{AO}{PO}$,$\therefore \frac{AO}{PO} = \frac{DA}{FA}$. $\therefore DA = \frac{20}{10\sqrt{5}} × 40 = 16\sqrt{5}$. $\therefore CD = DA - AC = 11\sqrt{5}$. $\because \angle AOP = \angle ADB$,$\angle ACO = \angle ECD$,$\therefore \triangle ACO \sim \triangle ECD$. $\therefore \frac{AO}{ED} = \frac{CO}{CD}$. $\therefore DE = \frac{11\sqrt{5}}{5\sqrt{5}} × 20 = 44$
10. (1)$\because AP$,BP分别切$\odot O$于点A,B,$\therefore OP$平分$\angle AOB$. $\therefore \angle AOP = \frac{1}{2}\angle AOB$.又$\because \overset{\frown}{AB} = \overset{\frown}{AB}$,$\therefore \angle ADB = \frac{1}{2}\angle AOB$. $\therefore \angle ADB = \angle AOP$ (2)如图,延长AO交$\odot O$于点F,连接DF,则$\angle ADF = 90°$. $\because AP$,BP分别切$\odot O$于点A,B,$\therefore PA \perp OA$. $\because C$为OP的中点,$\therefore PC = OC = AC = \frac{1}{2}OP$.又$\because AP = 10$,$\tan\angle AOP = \frac{1}{2}$,$\therefore AO = \frac{AP}{\tan\angle AOP} = 20$. $\therefore OP = \sqrt{AO^{2} + AP^{2}} = \sqrt{20^{2} + 10^{2}} = 10\sqrt{5}$. $\therefore AC = OC = \frac{1}{2}OP = 5\sqrt{5}$,$AF = 2AO = 40$. $\because AC = OC$,$\therefore \angle CAO = \angle AOC$.又$\because \angle PAO = \angle ADF = 90°$,$\cos\angle DAF = \frac{DA}{FA}$,$\cos\angle POA = \frac{AO}{PO}$,$\therefore \frac{AO}{PO} = \frac{DA}{FA}$. $\therefore DA = \frac{20}{10\sqrt{5}} × 40 = 16\sqrt{5}$. $\therefore CD = DA - AC = 11\sqrt{5}$. $\because \angle AOP = \angle ADB$,$\angle ACO = \angle ECD$,$\therefore \triangle ACO \sim \triangle ECD$. $\therefore \frac{AO}{ED} = \frac{CO}{CD}$. $\therefore DE = \frac{11\sqrt{5}}{5\sqrt{5}} × 20 = 44$
