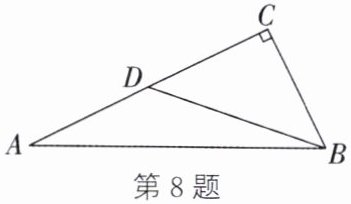
8. 如图,在$ Rt\triangle ABC$中,$\angle C=90°$,$ BC=\sqrt{5}$,$ D$是$ AC$上一点,连接$ BD$. 如果$\tan A=\frac{1}{2}$,$\tan \angle ABD=\frac{1}{3}$,那么$ CD=$
$\sqrt{5}$
.
答案:8.$\sqrt{5}$
解析:
解:在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$\tan A=\frac{BC}{AC}=\frac{1}{2}$,$BC=\sqrt{5}$,则$AC=2BC=2\sqrt{5}$。
设$CD=x$,则$AD=AC - CD=2\sqrt{5}-x$。
过点$D$作$DE\perp AB$于点$E$,设$DE=m$。
在$Rt\triangle ADE$中,$\tan A=\frac{DE}{AE}=\frac{1}{2}$,则$AE=2m$,$AD=\sqrt{AE^{2}+DE^{2}}=\sqrt{(2m)^{2}+m^{2}}=\sqrt{5}m$,即$2\sqrt{5}-x=\sqrt{5}m$,得$m=\frac{2\sqrt{5}-x}{\sqrt{5}}=2-\frac{x}{\sqrt{5}}$。
在$Rt\triangle BDE$中,$\tan\angle ABD=\frac{DE}{BE}=\frac{1}{3}$,则$BE=3m$。
在$Rt\triangle ABC$中,$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{(2\sqrt{5})^{2}+(\sqrt{5})^{2}}=5$。
因为$AB=AE + BE$,所以$2m + 3m=5$,即$5m=5$,$m=1$。
由$m=2-\frac{x}{\sqrt{5}}=1$,解得$x=\sqrt{5}$,即$CD=\sqrt{5}$。
$\sqrt{5}$
设$CD=x$,则$AD=AC - CD=2\sqrt{5}-x$。
过点$D$作$DE\perp AB$于点$E$,设$DE=m$。
在$Rt\triangle ADE$中,$\tan A=\frac{DE}{AE}=\frac{1}{2}$,则$AE=2m$,$AD=\sqrt{AE^{2}+DE^{2}}=\sqrt{(2m)^{2}+m^{2}}=\sqrt{5}m$,即$2\sqrt{5}-x=\sqrt{5}m$,得$m=\frac{2\sqrt{5}-x}{\sqrt{5}}=2-\frac{x}{\sqrt{5}}$。
在$Rt\triangle BDE$中,$\tan\angle ABD=\frac{DE}{BE}=\frac{1}{3}$,则$BE=3m$。
在$Rt\triangle ABC$中,$AB=\sqrt{AC^{2}+BC^{2}}=\sqrt{(2\sqrt{5})^{2}+(\sqrt{5})^{2}}=5$。
因为$AB=AE + BE$,所以$2m + 3m=5$,即$5m=5$,$m=1$。
由$m=2-\frac{x}{\sqrt{5}}=1$,解得$x=\sqrt{5}$,即$CD=\sqrt{5}$。
$\sqrt{5}$
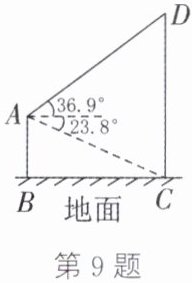
9. (2025·安徽)某公司为庆祝新产品上市,在甲楼与乙楼的楼顶之间悬挂彩带营造喜庆气氛. 如图,甲楼和乙楼分别用与水平地面垂直的线段$ AB$和$ CD$表示,彩带用线段$ AD$表示. 工作人员测得在点$ A$处看点$ C$的俯角为$23.8°$,看点$ D$的仰角为$36.9°$. 已知$ AB=13.20\ m$,求$ AD$的长(结果精确到$0.1\ m$,参考数据:$\sin 23.8°\approx 0.40$,$\cos 23.8°\approx 0.91$,$\tan 23.8°\approx 0.44$,$\sin 36.9°\approx 0.60$,$\cos 36.9°\approx 0.80$,$\tan 36.9°\approx 0.75$).

答案:
9.如图,过点A作$AE\perp CD$,垂足为E.由题意,易得四边形ABCE为矩形,$\therefore CE=AB=13.20$m.在$Rt\triangle ACE$中,$\tan\angle CAE=\frac{CE}{AE}$,$\therefore AE=\frac{CE}{\tan\angle CAE}=\frac{13.20}{\tan23.8^{\circ}}\approx\frac{13.20}{0.44}=30(m)$.在$Rt\triangle ADE$中,$\cos\angle DAE=\frac{AE}{AD}$,$\therefore AD=\frac{AE}{\cos\angle DAE}=\frac{30}{\cos36.9^{\circ}}\approx\frac{30}{0.80}=37.5(m).\therefore AD$的长约为$37.5$m
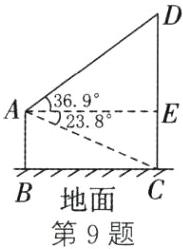
9.如图,过点A作$AE\perp CD$,垂足为E.由题意,易得四边形ABCE为矩形,$\therefore CE=AB=13.20$m.在$Rt\triangle ACE$中,$\tan\angle CAE=\frac{CE}{AE}$,$\therefore AE=\frac{CE}{\tan\angle CAE}=\frac{13.20}{\tan23.8^{\circ}}\approx\frac{13.20}{0.44}=30(m)$.在$Rt\triangle ADE$中,$\cos\angle DAE=\frac{AE}{AD}$,$\therefore AD=\frac{AE}{\cos\angle DAE}=\frac{30}{\cos36.9^{\circ}}\approx\frac{30}{0.80}=37.5(m).\therefore AD$的长约为$37.5$m

10. 如图,在$\triangle ABC$中,$\sin B=\frac{4}{5}$,点$ F$在$ BC$上,$ AB= AF=5$,过点$ F$作$ EF\perp CB$交$ AC$于点$ E$,且$ AE: EC=3:5$. 求$ BF$的长及$\sin C$的值.
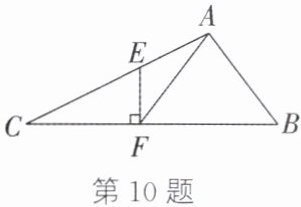

答案:10.过点A作$AD\perp CB$,垂足为D.$\because\sin B=\frac{4}{5}$,$\therefore$易得$\cos B=\frac{3}{5}$.在$Rt\triangle ABD$中,$BD=AB·\cos B=3.\because AB=AF$,$AD\perp CB$,$\therefore DF=BD=3$,$BF=2BD=6.\because EF\perp CB$,$AD\perp CB$,$\therefore EF// AD.\therefore\frac{DF}{CF}=\frac{AE}{EC}.\because AE:EC=3:5$,$\therefore CF=5.\therefore CD=CF+DF=5+3=8$.在$Rt\triangle ABD$中,$AD=AB·\sin B=5×\frac{4}{5}=4$.在$Rt\triangle ACD$中,$AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{4^{2}+8^{2}}=4\sqrt{5}.\therefore\sin C=\frac{AD}{AC}=\frac{\sqrt{5}}{5}$
解析:
解:过点$A$作$AD\perp CB$,垂足为$D$。
在$\triangle ABC$中,$\sin B = \frac{4}{5}$,则$\cos B = \sqrt{1 - (\frac{4}{5})^2} = \frac{3}{5}$。
在$Rt\triangle ABD$中,$BD = AB · \cos B = 5 × \frac{3}{5} = 3$。
因为$AB = AF$,$AD\perp CB$,所以$DF = BD = 3$,$BF = BD + DF = 3 + 3 = 6$。
因为$EF\perp CB$,$AD\perp CB$,所以$EF// AD$,则$\frac{AE}{EC} = \frac{DF}{CF}$。
已知$AE:EC = 3:5$,$DF = 3$,所以$\frac{3}{5} = \frac{3}{CF}$,解得$CF = 5$。
$CD = CF + DF = 5 + 3 = 8$。
在$Rt\triangle ABD$中,$AD = AB · \sin B = 5 × \frac{4}{5} = 4$。
在$Rt\triangle ACD$中,$AC = \sqrt{AD^2 + CD^2} = \sqrt{4^2 + 8^2} = 4\sqrt{5}$。
$\sin C = \frac{AD}{AC} = \frac{4}{4\sqrt{5}} = \frac{\sqrt{5}}{5}$。
综上,$BF$的长为$6$,$\sin C$的值为$\frac{\sqrt{5}}{5}$。
在$\triangle ABC$中,$\sin B = \frac{4}{5}$,则$\cos B = \sqrt{1 - (\frac{4}{5})^2} = \frac{3}{5}$。
在$Rt\triangle ABD$中,$BD = AB · \cos B = 5 × \frac{3}{5} = 3$。
因为$AB = AF$,$AD\perp CB$,所以$DF = BD = 3$,$BF = BD + DF = 3 + 3 = 6$。
因为$EF\perp CB$,$AD\perp CB$,所以$EF// AD$,则$\frac{AE}{EC} = \frac{DF}{CF}$。
已知$AE:EC = 3:5$,$DF = 3$,所以$\frac{3}{5} = \frac{3}{CF}$,解得$CF = 5$。
$CD = CF + DF = 5 + 3 = 8$。
在$Rt\triangle ABD$中,$AD = AB · \sin B = 5 × \frac{4}{5} = 4$。
在$Rt\triangle ACD$中,$AC = \sqrt{AD^2 + CD^2} = \sqrt{4^2 + 8^2} = 4\sqrt{5}$。
$\sin C = \frac{AD}{AC} = \frac{4}{4\sqrt{5}} = \frac{\sqrt{5}}{5}$。
综上,$BF$的长为$6$,$\sin C$的值为$\frac{\sqrt{5}}{5}$。
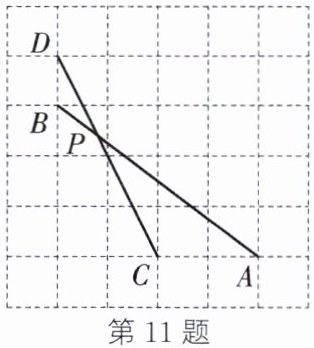
11. 如图,在方格纸中,每个小正方形的边长都相等,点$ A$,$ B$,$ C$,$ D$都在格点(小正方形的顶点)处,$ AB$与$ CD$相交于点$ P$,则$\cos \angle APC$的值为
(
A.$\frac{\sqrt{3}}{5}$
B.$\frac{2\sqrt{5}}{5}$
C.$\frac{2}{5}$
D.$\frac{\sqrt{5}}{5}$
(
B
)
A.$\frac{\sqrt{3}}{5}$
B.$\frac{2\sqrt{5}}{5}$
C.$\frac{2}{5}$
D.$\frac{\sqrt{5}}{5}$
答案:11.B