如果两个三角形的
$\therefore$
两边成比例
,并且夹角相等
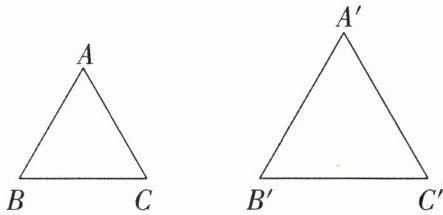
,那么这两个三角形相似. 用符号语言表述:如图,在$\triangle ABC$和$\triangle A'B'C'$中,$\because \frac{AB}{A'B'}=\frac{AC}{A'C'}$,$\angle A=\angle A'$
,$\therefore$
$\triangle ABC\sim\triangle A'B'C'$
.
答案:两边成比例 夹角相等 $\angle A=\angle A'$ $\triangle ABC\sim\triangle A'B'C'$
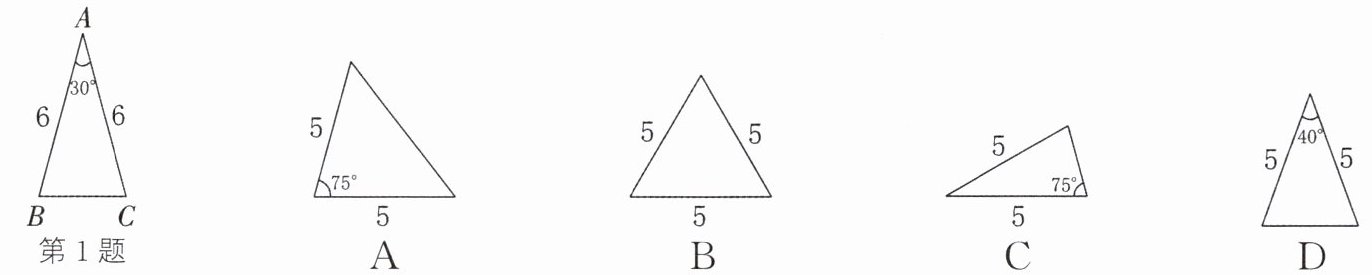
1. 如图所示为$\triangle ABC$,下列四个三角形中,与$\triangle ABC$相似的为 (
C
)
答案:1. C
解析:
解:在$\triangle ABC$中,$AB=AC=6$,$\angle A=30°$,
$\angle B=\angle C=\frac{180° - 30°}{2}=75°$,
$\triangle ABC$的三个内角分别为$30°$,$75°$,$75°$。
选项C的三角形中,有两个内角为$75°$,则第三个内角为$180° - 75° - 75°=30°$,
三个内角分别为$30°$,$75°$,$75°$,与$\triangle ABC$的内角对应相等,
所以选项C的三角形与$\triangle ABC$相似。
C
$\angle B=\angle C=\frac{180° - 30°}{2}=75°$,
$\triangle ABC$的三个内角分别为$30°$,$75°$,$75°$。
选项C的三角形中,有两个内角为$75°$,则第三个内角为$180° - 75° - 75°=30°$,
三个内角分别为$30°$,$75°$,$75°$,与$\triangle ABC$的内角对应相等,
所以选项C的三角形与$\triangle ABC$相似。
C
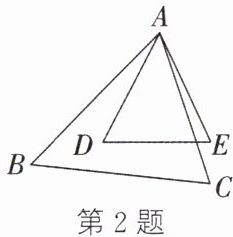
2. 如图,在$\triangle ABC$和$\triangle ADE$中,$\angle BAC = \angle D$,要使$\triangle ABC$与$\triangle ADE$相似,还需满足下列条件中的 (
A.$\frac{AC}{AD}=\frac{AB}{AE}$
B.$\frac{AC}{AD}=\frac{BC}{DE}$
C.$\frac{AC}{AD}=\frac{AB}{DE}$
D.$\frac{AC}{AD}=\frac{BC}{AE}$
C
)
A.$\frac{AC}{AD}=\frac{AB}{AE}$
B.$\frac{AC}{AD}=\frac{BC}{DE}$
C.$\frac{AC}{AD}=\frac{AB}{DE}$
D.$\frac{AC}{AD}=\frac{BC}{AE}$
答案:2. C
解析:
证明:已知在$\triangle ABC$和$\triangle ADE$中,$\angle BAC = \angle D$。
若要使$\triangle ABC \sim \triangle ADE$,根据“两边成比例且夹角相等的两个三角形相似”,需满足夹$\angle BAC$与$\angle D$的两边对应成比例。
$\angle BAC$的两边为$AB$、$AC$,$\angle D$的两边为$DE$、$AD$,因此需$\frac{AC}{AD}=\frac{AB}{DE}$。
答案:C
若要使$\triangle ABC \sim \triangle ADE$,根据“两边成比例且夹角相等的两个三角形相似”,需满足夹$\angle BAC$与$\angle D$的两边对应成比例。
$\angle BAC$的两边为$AB$、$AC$,$\angle D$的两边为$DE$、$AD$,因此需$\frac{AC}{AD}=\frac{AB}{DE}$。
答案:C
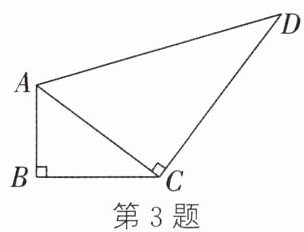
3. 如图,$AB\perp CB$于点$B$,$AC\perp CD$于点$C$,$AB = 6$,$AC = 10$. 当$CD =$
$\frac{40}{3}$
时,$\triangle ABC \backsim \triangle ACD$.
答案:3. $\frac{40}{3}$
解析:
解:
∵ $AB \perp CB$,$AC \perp CD$,
∴ $\angle B = \angle ACD = 90°$。
在 $Rt\triangle ABC$ 中,$AB = 6$,$AC = 10$,
由勾股定理得:$BC = \sqrt{AC^2 - AB^2} = \sqrt{10^2 - 6^2} = 8$。
若 $\triangle ABC \backsim \triangle ACD$,则 $\frac{AB}{AC} = \frac{BC}{CD}$,
即 $\frac{6}{10} = \frac{8}{CD}$,解得 $CD = \frac{8 × 10}{6} = \frac{40}{3}$。
$\frac{40}{3}$
∵ $AB \perp CB$,$AC \perp CD$,
∴ $\angle B = \angle ACD = 90°$。
在 $Rt\triangle ABC$ 中,$AB = 6$,$AC = 10$,
由勾股定理得:$BC = \sqrt{AC^2 - AB^2} = \sqrt{10^2 - 6^2} = 8$。
若 $\triangle ABC \backsim \triangle ACD$,则 $\frac{AB}{AC} = \frac{BC}{CD}$,
即 $\frac{6}{10} = \frac{8}{CD}$,解得 $CD = \frac{8 × 10}{6} = \frac{40}{3}$。
$\frac{40}{3}$
4. 如图,点$D$,$E$分别在$AB$,$AC$上. 若$AB = 2AE$,$AC = 2AD$,$DE = 5$,则$BC =$
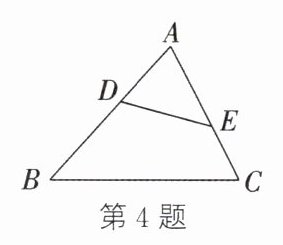
10
.
答案:4. 10
解析:
证明:在$\triangle ADE$和$\triangle ACB$中,
$\because AB = 2AE$,$AC = 2AD$,
$\therefore \frac{AD}{AC} = \frac{AE}{AB} = \frac{1}{2}$。
又$\because \angle DAE = \angle CAB$,
$\therefore \triangle ADE \sim \triangle ACB$(两边成比例且夹角相等的两个三角形相似)。
$\therefore \frac{DE}{BC} = \frac{AD}{AC} = \frac{1}{2}$。
$\because DE = 5$,
$\therefore BC = 2DE = 2×5 = 10$。
10
$\because AB = 2AE$,$AC = 2AD$,
$\therefore \frac{AD}{AC} = \frac{AE}{AB} = \frac{1}{2}$。
又$\because \angle DAE = \angle CAB$,
$\therefore \triangle ADE \sim \triangle ACB$(两边成比例且夹角相等的两个三角形相似)。
$\therefore \frac{DE}{BC} = \frac{AD}{AC} = \frac{1}{2}$。
$\because DE = 5$,
$\therefore BC = 2DE = 2×5 = 10$。
10
5. 如图,在等边三角形$ABC$中,点$D$,$E$分别在边$AC$,$AB$上,且$\frac{AD}{AC}=\frac{1}{3}$,$AE = BE$,连接$DE$,$BD$. 求证:$\angle AED = \angle CBD$.
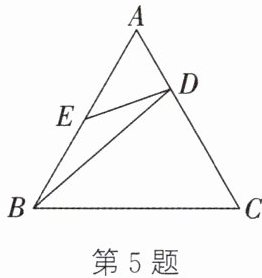

答案:5. $\because \triangle ABC$为等边三角形,$\therefore \angle A=\angle C=60°$,$BC=AB$。
$\because AE = BE$,$\therefore AB = 2AE$。$\therefore BC = 2AE$。$\because \frac{AD}{AC}=\frac{1}{3}$,
$\therefore CD = 2AD$。$\therefore \frac{AD}{CD}=\frac{AE}{CB}=\frac{1}{2}$。$\because \angle A=\angle C$,$\therefore \triangle AED\sim$
$\triangle CBD$。$\therefore \angle AED=\angle CBD$
$\because AE = BE$,$\therefore AB = 2AE$。$\therefore BC = 2AE$。$\because \frac{AD}{AC}=\frac{1}{3}$,
$\therefore CD = 2AD$。$\therefore \frac{AD}{CD}=\frac{AE}{CB}=\frac{1}{2}$。$\because \angle A=\angle C$,$\therefore \triangle AED\sim$
$\triangle CBD$。$\therefore \angle AED=\angle CBD$