2. 数学家皮尔逊(Pearson)曾在试验中掷硬币 24 000 次,正面朝上的次数是 12 012 次。据此,估计掷硬币正面朝上的概率是
0.5
。答案:0.5
3. 从某品种玉米种子中抽取 6 批,在同一条件下进行发芽试验,有关数据如下:

该玉米种子发芽的概率约为

该玉米种子发芽的概率约为
0.8
(精确到 0.1)。答案:3.0.8
4. 从车站到书城有 $ A_1 $、$ A_2 $、$ A_3 $、$ A_4 $ 四条路线可走,从书城到广场有 $ B_1 $、$ B_2 $、$ B_3 $ 三条路线可走,随机选择一条从车站出发经过书城到达广场的行走路线。
(1)画树状图分析所有可能选择的路线;
(2)恰好选到经过路线 $ B_1 $ 的概率是多少?
(1)画树状图分析所有可能选择的路线;
(2)恰好选到经过路线 $ B_1 $ 的概率是多少?
答案:
解: (1)列树状图如下:
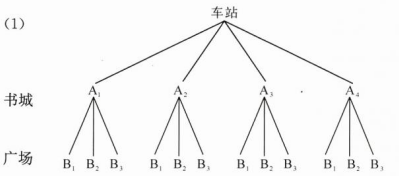
(2)从车站到书城共有12条路线并且它们是等可能的,经过${B}_1$的路线有4条。
∴P(经过${B}_1)=\frac {4}{12}=\frac {1}{3}$
答:恰好选到经过路线${B}_1$的概率是$\frac {1}{3}。$
解: (1)列树状图如下:

(2)从车站到书城共有12条路线并且它们是等可能的,经过${B}_1$的路线有4条。
∴P(经过${B}_1)=\frac {4}{12}=\frac {1}{3}$
答:恰好选到经过路线${B}_1$的概率是$\frac {1}{3}。$
在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表。

(1)计算表中 $ a $、$ b $ 的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有 87%的麦芽可以成活,现有 100 kg 麦种,大约有多少千克的麦种可以成活为麦苗?

(1)计算表中 $ a $、$ b $ 的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有 87%的麦芽可以成活,现有 100 kg 麦种,大约有多少千克的麦种可以成活为麦苗?
答案:解:(1)a =1900÷2000=0.950
b=2850÷3000= 0.950
(2)当试验次数逐渐增多时,发现种子发芽的频率在常数0.950附近摆动,
∴由此估计该麦种的发芽概率是0.95。
$(3)100×0.95×87\%=82.65\ \mathrm {kg}$
答:大约有82.65千克的麦种可以成活为麦苗。
b=2850÷3000= 0.950
(2)当试验次数逐渐增多时,发现种子发芽的频率在常数0.950附近摆动,
∴由此估计该麦种的发芽概率是0.95。
$(3)100×0.95×87\%=82.65\ \mathrm {kg}$
答:大约有82.65千克的麦种可以成活为麦苗。