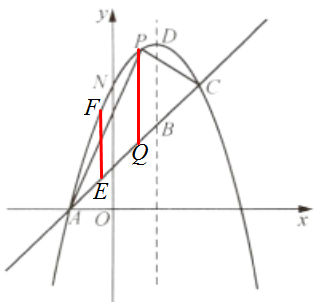
18. (12 分)如图,已知二次函数$y = -x^{2} + bx + c$的图像是顶点为$D$的抛物线,且与一直线相交于点$A(-1,0)$、$C(2,3)$,与$y$轴交于点$N$.
(1)求这个二次函数的表达式及直线$AC$相应的函数表达式.
(2)设点$M$的坐标为$(3,m)$,当$m$取何值时,$MN + MD$的值最小?
(3)若抛物线的对称轴与直线$AC$相交于点$B$,$E$为直线$AC$上的任意一点,过点$E$作$EF // BD$,交抛物线于点$F$,以$B$、$D$、$E$、$F$为顶点的四边形能否为平行四边形?若能,求点$E$的坐标;若不能,请说明理由.
(4)若$P$是抛物线上位于直线$AC$上方的一个动点,求$\triangle APC$面积的最大值.

(1)求这个二次函数的表达式及直线$AC$相应的函数表达式.
(2)设点$M$的坐标为$(3,m)$,当$m$取何值时,$MN + MD$的值最小?
(3)若抛物线的对称轴与直线$AC$相交于点$B$,$E$为直线$AC$上的任意一点,过点$E$作$EF // BD$,交抛物线于点$F$,以$B$、$D$、$E$、$F$为顶点的四边形能否为平行四边形?若能,求点$E$的坐标;若不能,请说明理由.
(4)若$P$是抛物线上位于直线$AC$上方的一个动点,求$\triangle APC$面积的最大值.

答案:
解:(1)由二次函数y=-x²+bx+c 的图像经过点A(-1,0),C(2,3)
$\begin{cases}{-1-b+c=0 } \\{-4+2b+c=3} \end{cases} $解得$\begin{cases}{b=2}\\{c=3}\end{cases}$
∴函数表达式为y= -x²+ 2x +3
由直线AC经过点A(-1,0),C(2,3)
可得函数表达式为y=x+ 1
(2)由y= -x²+2x+ 3,得N(0,3),D(1,4)
点D关于过点(3,0)且与y轴平行的直线的对称点D'的坐标为(5,4)
连接ND',则ND'的函数表达式为$y=\frac {1}{5}x+ 3$
ND'交一次函数x = 3的图像于点M(3,$\frac {18}{5})$
即$m=\frac {18}{5},$此时MN+MD的值最小
(3)二次函数y= -x²+2x+3的图像的对称轴为过点(1,0)且与y轴平行的直线
因此B(1,2),D(1,4),BD= 2
若以B、D、E、F 为顶点的四边形是平行四边形,且EF//BD
则EF= BD
设点E、F 的坐标分别为(t,t+1)、(t,-t²+2t+3)
则|(-t²+2t+3)-(t+1)|=2
解得${t}_1= 0,$${t}_2= 1($舍去),${t}_3=\frac {1+\sqrt{17}}{2},$${t}_4=\frac {1-\sqrt{17}}{2} $
∴${E}_1(0,$1),${E}_2(\frac {1+\sqrt{17}}{2},$$\frac {3+\sqrt{17}}{2}),$${E}_3(\frac {1-\sqrt{17}}{2},$$\frac {3-\sqrt{17}}{2})$
(4)过点P 作PQ//y轴,交AC于点Q
设点P 的坐标为(a,-a²+ 2a+ 3),则点Q 的坐标为(a,a + 1)
∵点P 在AC上方
∴PQ=(-a²+2a+3)- (a+1)= -a²+a+2
∴$S_{△APC}= S_{△APQ}+ S_{△CPQ}$
$=\frac {1}{2}(-a²+a+2) · [2-(-1)]$
$=-\frac {3}{2}(a-\frac {1}{2})²+\frac {27}{8}$
∴当$a=\frac {1}{2}$时,$S_{△APC}$的最大值为$\frac {27}{8}$
解:(1)由二次函数y=-x²+bx+c 的图像经过点A(-1,0),C(2,3)
$\begin{cases}{-1-b+c=0 } \\{-4+2b+c=3} \end{cases} $解得$\begin{cases}{b=2}\\{c=3}\end{cases}$
∴函数表达式为y= -x²+ 2x +3
由直线AC经过点A(-1,0),C(2,3)
可得函数表达式为y=x+ 1
(2)由y= -x²+2x+ 3,得N(0,3),D(1,4)
点D关于过点(3,0)且与y轴平行的直线的对称点D'的坐标为(5,4)
连接ND',则ND'的函数表达式为$y=\frac {1}{5}x+ 3$
ND'交一次函数x = 3的图像于点M(3,$\frac {18}{5})$
即$m=\frac {18}{5},$此时MN+MD的值最小
(3)二次函数y= -x²+2x+3的图像的对称轴为过点(1,0)且与y轴平行的直线
因此B(1,2),D(1,4),BD= 2
若以B、D、E、F 为顶点的四边形是平行四边形,且EF//BD
则EF= BD
设点E、F 的坐标分别为(t,t+1)、(t,-t²+2t+3)
则|(-t²+2t+3)-(t+1)|=2
解得${t}_1= 0,$${t}_2= 1($舍去),${t}_3=\frac {1+\sqrt{17}}{2},$${t}_4=\frac {1-\sqrt{17}}{2} $
∴${E}_1(0,$1),${E}_2(\frac {1+\sqrt{17}}{2},$$\frac {3+\sqrt{17}}{2}),$${E}_3(\frac {1-\sqrt{17}}{2},$$\frac {3-\sqrt{17}}{2})$
(4)过点P 作PQ//y轴,交AC于点Q
设点P 的坐标为(a,-a²+ 2a+ 3),则点Q 的坐标为(a,a + 1)
∵点P 在AC上方
∴PQ=(-a²+2a+3)- (a+1)= -a²+a+2
∴$S_{△APC}= S_{△APQ}+ S_{△CPQ}$
$=\frac {1}{2}(-a²+a+2) · [2-(-1)]$
$=-\frac {3}{2}(a-\frac {1}{2})²+\frac {27}{8}$
∴当$a=\frac {1}{2}$时,$S_{△APC}$的最大值为$\frac {27}{8}$
