17. (10 分)如图,在$\triangle ABC$中,$AB = AC$,$AD$为边$BC$上的中线,$DE \perp AB$,垂足为$E$.
(1) 求证:$\triangle BDE \backsim \triangle CAD$;
(2) 若$AB = 13$,$BC = 10$,求线段$DE$的长.

(1) 求证:$\triangle BDE \backsim \triangle CAD$;
(2) 若$AB = 13$,$BC = 10$,求线段$DE$的长.

答案:证明: (1)∵AB=AC,AD是边BC的中线
∴∠B=∠C,AD⊥BC
∵DE⊥AB
∴∠ADC=∠BED=90°
又∵∠B=∠C
∴△BDE∽△CAD
(2)∵AB=AC,AD是边BC的中线
∴AC=13,BD=CD=5
∵△BDE∽△CAD
∴$\frac {BE}{CD}=\frac {BD}{AC}$
∴$\frac {BE}{5}=\frac {5}{13}$
∴$BE =\frac {25}{13}$
∴$DE=\sqrt{BD² - BE²}=\frac {60}{13}$
∴∠B=∠C,AD⊥BC
∵DE⊥AB
∴∠ADC=∠BED=90°
又∵∠B=∠C
∴△BDE∽△CAD
(2)∵AB=AC,AD是边BC的中线
∴AC=13,BD=CD=5
∵△BDE∽△CAD
∴$\frac {BE}{CD}=\frac {BD}{AC}$
∴$\frac {BE}{5}=\frac {5}{13}$
∴$BE =\frac {25}{13}$
∴$DE=\sqrt{BD² - BE²}=\frac {60}{13}$
18. (12 分)将正方形纸片$ABCD$对折,得到折痕$EF$,再沿$CE$折叠,得到折痕$CE$,然后将正方形纸片折叠,使$BC$落在$CE$上,得到折痕$CG$,点$B$翻折至点$H$处. 试说明点$G$为线段$AB$的黄金分割点.


答案:
解:设正方形的边长为2a,易得ED=a,$CE=\sqrt{5}a$
过点H作MN//AD,分别交AB,CD于点M,N
则△CNH∽△CDE
∴$\frac {NH}{ED}=\frac {CH}{CE}$
∵CH= 2a,ED=a,$CE=\sqrt{5}a$
∴$NH=\frac {2\sqrt{5}}{5}a$
∴$MH= 2a-\frac {2\sqrt{5}}{5}a$
由上述可得,∠HMG =∠CNH=∠CHG= 90°
得∠MHG=∠NCH,△HMG∽△CNH
∴△HMG∽△CDE
∴$\frac {HG}{EC}=\frac {MH}{CD}$
则$HG=\frac {\sqrt{5}}{2}(2a-\frac {2\sqrt{5}}{5}a)=(\sqrt{5}-1)a$
∴$BG= HG=\frac {\sqrt{5}-1}{2}AB$
∴点G 为AB的黄金分割点
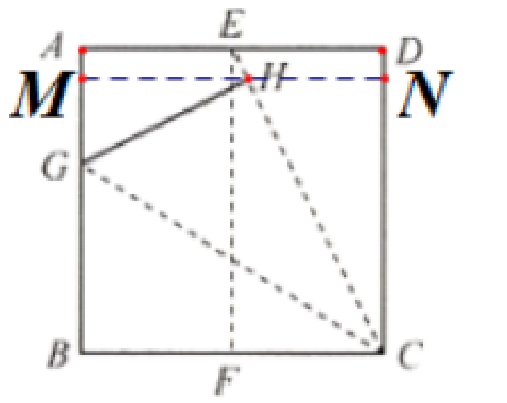
解:设正方形的边长为2a,易得ED=a,$CE=\sqrt{5}a$
过点H作MN//AD,分别交AB,CD于点M,N
则△CNH∽△CDE
∴$\frac {NH}{ED}=\frac {CH}{CE}$
∵CH= 2a,ED=a,$CE=\sqrt{5}a$
∴$NH=\frac {2\sqrt{5}}{5}a$
∴$MH= 2a-\frac {2\sqrt{5}}{5}a$
由上述可得,∠HMG =∠CNH=∠CHG= 90°
得∠MHG=∠NCH,△HMG∽△CNH
∴△HMG∽△CDE
∴$\frac {HG}{EC}=\frac {MH}{CD}$
则$HG=\frac {\sqrt{5}}{2}(2a-\frac {2\sqrt{5}}{5}a)=(\sqrt{5}-1)a$
∴$BG= HG=\frac {\sqrt{5}-1}{2}AB$
∴点G 为AB的黄金分割点
