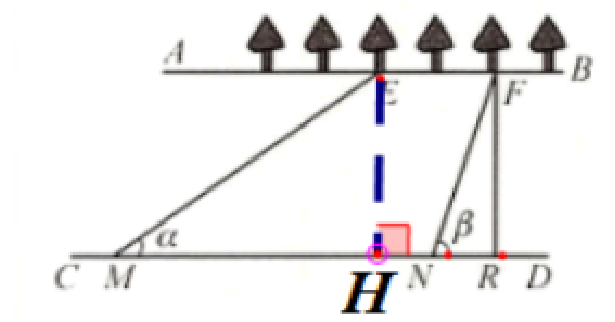
18. (10 分)综合实践课上,小明所在的小组要测量某河道的宽度.如图,已知该河的两岸 AB、CD 相互平行,河岸 AB 上有一排大树,相邻两棵大树之间的距离均为 10 m.小明先用测角仪在河岸 CD 的 M 处测得∠α = 36°,然后沿河岸走 50 m 到达点 N,测得∠β = 72°.请你根据这些数据算出河宽 FR(精确到 1 m;参考数据:sin 36°≈0.59,cos 36°≈0.81,tan 36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan 72°≈3.08).


答案:
解:过点E作EH⊥CD,垂足为点H
由题意EF=10×2=20m,HR=EF=20m
设河宽为$x\ \mathrm {m},$即FR=EH=x
$MH=\frac {EH}{tan α}≈\frac {x}{0.73}$
$NR=\frac {FP}{tan β}≈\frac {x}{3.08}$
∵MR = MH+ HR= MN+ NR
∴$\frac {x}{0.73}+20=\frac {x}{3.08}+50$
∴x≈29
答:河宽约为29m。
解:过点E作EH⊥CD,垂足为点H
由题意EF=10×2=20m,HR=EF=20m
设河宽为$x\ \mathrm {m},$即FR=EH=x
$MH=\frac {EH}{tan α}≈\frac {x}{0.73}$
$NR=\frac {FP}{tan β}≈\frac {x}{3.08}$
∵MR = MH+ HR= MN+ NR
∴$\frac {x}{0.73}+20=\frac {x}{3.08}+50$
∴x≈29
答:河宽约为29m。

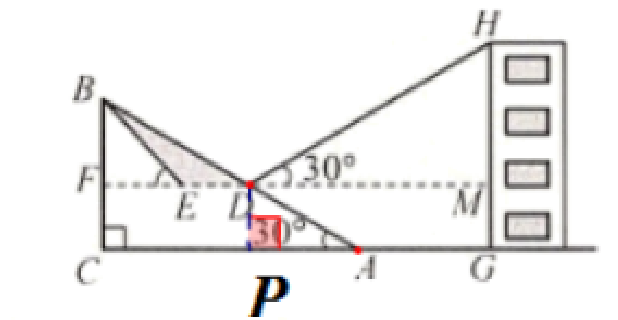
19. (10 分)如图,已知斜坡 AB 长 60 m,坡角(即∠BAC)为 30°,BC⊥AC,现计划在斜坡的中点 D 处挖去部分坡体(用阴影表示)修建一个平行于水平线 CA 的平台 DE 和一条新的斜坡 BE(都精确到 0.1 m;参考数据:$\sqrt{3}$≈1.732).
(1) 若修建的斜坡 BE 的坡角(即∠BEF)不大于 45°,则平台 DE 的长最大为多少米?
(2) 一座建筑物 GH 距离点 A 27 m(即 AG = 27 m),小明在点 D 处测得建筑物顶部 H 的仰角(即∠HDM)为 30°.点 B、C、A、G、H 在同一个平面内,点 C、A、G 在同一条直线上,且 HG⊥CG,则建筑物的高 GH 为多少米?

(1) 若修建的斜坡 BE 的坡角(即∠BEF)不大于 45°,则平台 DE 的长最大为多少米?
(2) 一座建筑物 GH 距离点 A 27 m(即 AG = 27 m),小明在点 D 处测得建筑物顶部 H 的仰角(即∠HDM)为 30°.点 B、C、A、G、H 在同一个平面内,点 C、A、G 在同一条直线上,且 HG⊥CG,则建筑物的高 GH 为多少米?

答案:
解: (1)∵点D为AB的中点
∴BD= AD= 30m
∵FM//CG
∴∠BDF=∠BAC= 30°
BF=sin 30°×BD=15m
$FD= cos 30°×BD= 15\sqrt{3}m$
若∠BEF=45°,EF=BF= 15m
∴当∠BEF≤45°,EF≥15m
∴DE≤11.0m
(2)过点D作DP⊥CG,垂足为点P
∵∠DAC=30°
∴DP=sin 30°×AD=15m,
$AP= cos 30°×AD =15\sqrt{3}m$
$DM=AP+AG=(15\sqrt{3}+27)m$
∵∠HDM=30°
∴HM=tan 30°×DM≈30.6m
∴HG= HM+ MG=45.6m
解: (1)∵点D为AB的中点
∴BD= AD= 30m
∵FM//CG
∴∠BDF=∠BAC= 30°
BF=sin 30°×BD=15m
$FD= cos 30°×BD= 15\sqrt{3}m$
若∠BEF=45°,EF=BF= 15m
∴当∠BEF≤45°,EF≥15m
∴DE≤11.0m
(2)过点D作DP⊥CG,垂足为点P
∵∠DAC=30°
∴DP=sin 30°×AD=15m,
$AP= cos 30°×AD =15\sqrt{3}m$
$DM=AP+AG=(15\sqrt{3}+27)m$
∵∠HDM=30°
∴HM=tan 30°×DM≈30.6m
∴HG= HM+ MG=45.6m
