活动一:思一思 做一做
(1) 请填表并在平面直角坐标系(图 5 - 5)中画出二次函数$y = x^{2}$、$y = (x + 1)^{2}$、$y = (x + 1)^{2} + 2$的图像.
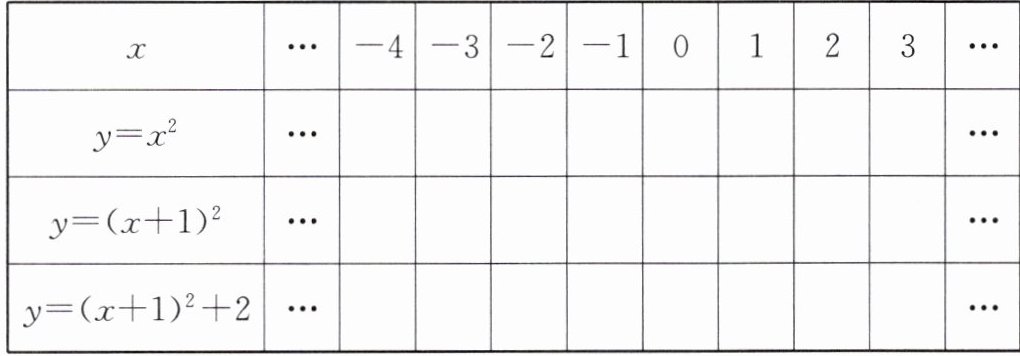
(2) 观察表格中的数值及函数表达式,说出它们的开口方向、对称轴和顶点坐标.
(3) 观察 3 个函数的图像,它们之间有什么关系吗?

(1) 请填表并在平面直角坐标系(图 5 - 5)中画出二次函数$y = x^{2}$、$y = (x + 1)^{2}$、$y = (x + 1)^{2} + 2$的图像.

(2) 观察表格中的数值及函数表达式,说出它们的开口方向、对称轴和顶点坐标.
(3) 观察 3 个函数的图像,它们之间有什么关系吗?

答案:
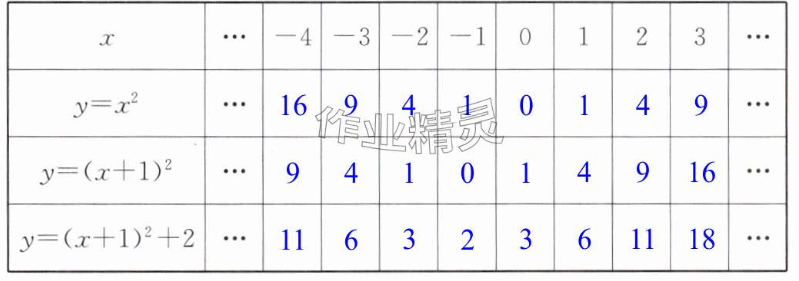
解:y=x²的开口方向向上,对称轴为y轴,顶点坐标为(0,0)
y= (x+1)²的开口方向向上,对称轴为直线x=-1,顶点坐标为(-1,0)
y= (x+ 1)² + 2的开口方向向上,对称轴为直线x=-1,顶点坐标为(-1,2)
解:y= (x+1)²可以看成是y = x²向左平移1个单位长度得到的,
y= (x+1)²+2可以看成是y=(x+1)²向上平移2个单位长度得到的。
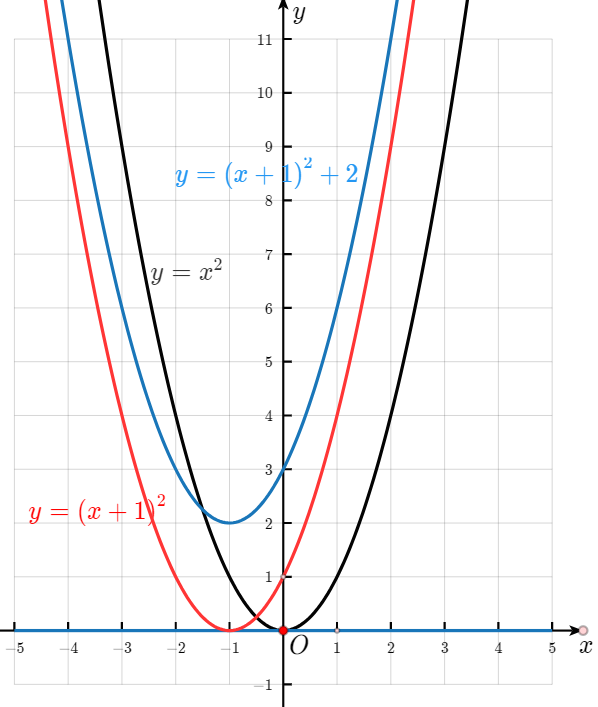

解:y=x²的开口方向向上,对称轴为y轴,顶点坐标为(0,0)
y= (x+1)²的开口方向向上,对称轴为直线x=-1,顶点坐标为(-1,0)
y= (x+ 1)² + 2的开口方向向上,对称轴为直线x=-1,顶点坐标为(-1,2)
解:y= (x+1)²可以看成是y = x²向左平移1个单位长度得到的,
y= (x+1)²+2可以看成是y=(x+1)²向上平移2个单位长度得到的。

活动二:想一想 做一做
1. 二次函数$y = x^{2} + 2x + 3$的图像是抛物线吗?如何画出二次函数$y = x^{2} + 2x + 3$的图像?
2. 你能把二次函数$y = ax^{2} + bx + c$化成$y = a(x + h)^{2} + k$的形式吗?试一试.
3. 通过以上探究,你能说说二次函数$y = ax^{2} + bx + c$有哪些性质吗?试一试.
1. 二次函数$y = x^{2} + 2x + 3$的图像是抛物线吗?如何画出二次函数$y = x^{2} + 2x + 3$的图像?
2. 你能把二次函数$y = ax^{2} + bx + c$化成$y = a(x + h)^{2} + k$的形式吗?试一试.
3. 通过以上探究,你能说说二次函数$y = ax^{2} + bx + c$有哪些性质吗?试一试.
答案:
解:是抛物线。将二次函数表达式先配方,y= (x + 1)²+2
函数图像如下
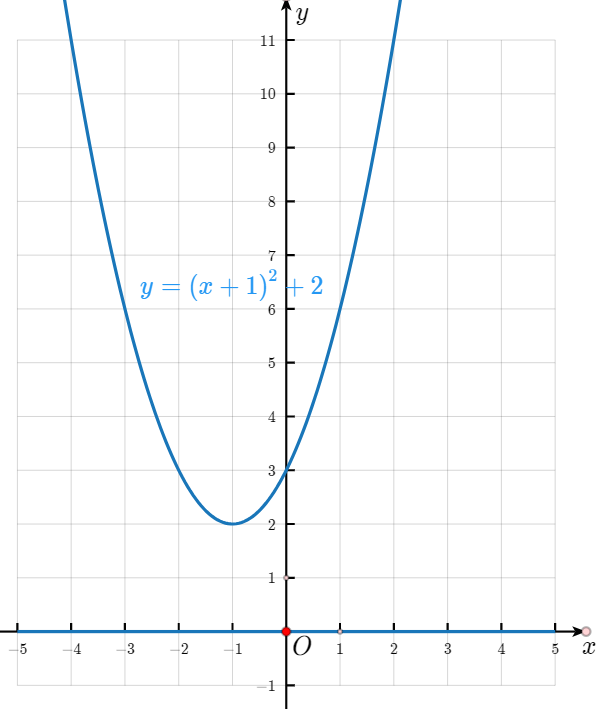
解:$y=ax²+bx+c=a(x²+\frac {b}{a}x)+c=a(x+\frac {b}{2a})²+\frac {4ac-b²}{4a}$
解:二次函数的对称轴为直线$x = -\frac {b}{2a}$
顶点坐标为$(-\frac {b}{2a},$$\frac {4ac-b²}{4a})$
解:是抛物线。将二次函数表达式先配方,y= (x + 1)²+2
函数图像如下

解:$y=ax²+bx+c=a(x²+\frac {b}{a}x)+c=a(x+\frac {b}{2a})²+\frac {4ac-b²}{4a}$
解:二次函数的对称轴为直线$x = -\frac {b}{2a}$
顶点坐标为$(-\frac {b}{2a},$$\frac {4ac-b²}{4a})$