1. 如图,某农场计划建造一个矩形养殖场,该矩形养殖场一面靠墙(墙的长度为$10{m}$),另外三面用栅栏围成,中间再用栅栏把它分成两个面积之比为$1:2$的矩形,已知栅栏的总长度为$24{m}$,设较小矩形的短边为$x{m}$.
(1)若矩形养殖场的总面积为$36{m^{2}}$,求此时$x$的值.
(2)当$x$为多少时,矩形养殖场的总面积最大?最大值为多少?

(1)若矩形养殖场的总面积为$36{m^{2}}$,求此时$x$的值.
(2)当$x$为多少时,矩形养殖场的总面积最大?最大值为多少?

答案:
解:(1)如图进行标记
∵BC=x,矩形CDEF 的面积是矩形BCFA面积的2倍
∴CD=2x
∴BD=3x,$AB=CF=DE=\frac {1}{3} (24-BD)=8-x$
根据题意,得3x(8-x)= 36
解得$x_{1}=2,$$x_{2}=6($不合题意,舍去)
此时x的值为$2\ \mathrm {m} $
(2)设矩形养殖场的总面积为S
由(1)得$S=3x(8-x)=-3(x-4)^2+48$
∵墙的长度为$10\ \mathrm {m}$
∴$0\lt 3x≤10$
∴$0\lt x≤ \frac {10}{3}$
∵$-3\lt 0$
∴$x\lt 4$时,S 随着x的增大而增大
∴当$x=\frac {10}{3} $时,S 取最大值,最大值为$-3×(\frac {10}{3} -4)^2 +48=\frac {140}{3} (\ \mathrm {m^2})$
当$x=\frac {10}{3} $时,矩形养殖场的总面积最大,最大值为$ \frac {140}{3}\ \mathrm {m^2} $
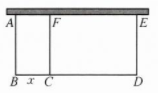
解:(1)如图进行标记
∵BC=x,矩形CDEF 的面积是矩形BCFA面积的2倍
∴CD=2x
∴BD=3x,$AB=CF=DE=\frac {1}{3} (24-BD)=8-x$
根据题意,得3x(8-x)= 36
解得$x_{1}=2,$$x_{2}=6($不合题意,舍去)
此时x的值为$2\ \mathrm {m} $
(2)设矩形养殖场的总面积为S
由(1)得$S=3x(8-x)=-3(x-4)^2+48$
∵墙的长度为$10\ \mathrm {m}$
∴$0\lt 3x≤10$
∴$0\lt x≤ \frac {10}{3}$
∵$-3\lt 0$
∴$x\lt 4$时,S 随着x的增大而增大
∴当$x=\frac {10}{3} $时,S 取最大值,最大值为$-3×(\frac {10}{3} -4)^2 +48=\frac {140}{3} (\ \mathrm {m^2})$
当$x=\frac {10}{3} $时,矩形养殖场的总面积最大,最大值为$ \frac {140}{3}\ \mathrm {m^2} $

2. 某校数学兴趣小组经过市场调查,整理出某种商品在第$x(1 \leqslant x \leqslant 90)$天的售价与销量的相关信息如下表:

已知该商品的进价为每件$30$元,设销售该商品每天的利润为$y$元.
(1)求$y$与$x$之间的函数表达式.
(2)第几天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,日销售利润不低于$4800$元的共有多少天?请直接写出结果.

已知该商品的进价为每件$30$元,设销售该商品每天的利润为$y$元.
(1)求$y$与$x$之间的函数表达式.
(2)第几天的销售利润最大?最大利润是多少?
(3)该商品在销售过程中,日销售利润不低于$4800$元的共有多少天?请直接写出结果.
答案:解:(1) 当$1≤x\lt 50$时,$y=(200-2x)(x+40-30)=-2x^2+180x+2000;$
当50≤x≤90时y=(200-2x)(90-30)=-120x+12000
综上所述:$y=\begin{cases}{-2x^2+180x+2000(1≤x\lt 50)}\\{-120x+12000(50≤x≤90)}\end{cases}$
(2) 当$1≤x\lt 50$时,二次函数的图像开口向下;
当x=45时,$y_{最大值}=6050$
当50≤x≤90时,y随x的增大而减小
当x=50时,$y_{最大值}=6000$
综上所述,该商品在第45天时,当天销售利润最大,最大利润是6050元
(3) 当20≤x≤60时,即共有41天,每天销售利润不低于4800元
当50≤x≤90时y=(200-2x)(90-30)=-120x+12000
综上所述:$y=\begin{cases}{-2x^2+180x+2000(1≤x\lt 50)}\\{-120x+12000(50≤x≤90)}\end{cases}$
(2) 当$1≤x\lt 50$时,二次函数的图像开口向下;
当x=45时,$y_{最大值}=6050$
当50≤x≤90时,y随x的增大而减小
当x=50时,$y_{最大值}=6000$
综上所述,该商品在第45天时,当天销售利润最大,最大利润是6050元
(3) 当20≤x≤60时,即共有41天,每天销售利润不低于4800元