1. 在如图所示的平面直角坐标系中,分别画出下列函数的图像.
(1)$y = 2x^{2}$; (2)$y = -\frac{1}{2}x^{2}$.

(1)$y = 2x^{2}$; (2)$y = -\frac{1}{2}x^{2}$.

答案:
(1) $y = 2x^2$:
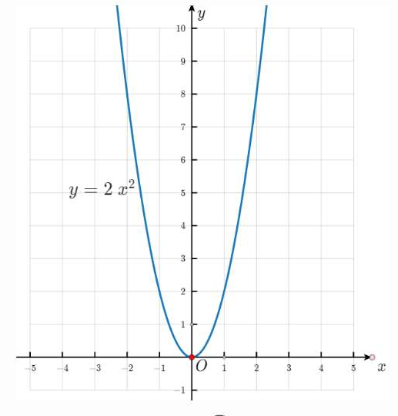
(2) $y = -\frac{1}{2}x^2$:
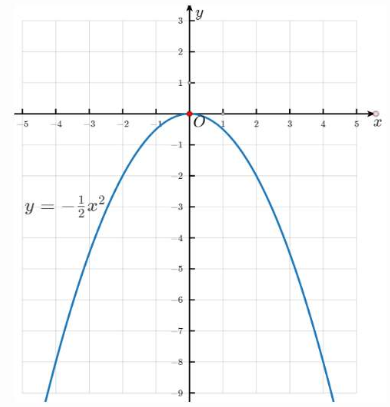
(1) $y = 2x^2$:

(2) $y = -\frac{1}{2}x^2$:

2. 观察二次函数$y = 2x^{2}$、$y = -\frac{1}{2}x^{2}$的图像,回答下列问题:
(1)二次函数$y = 2x^{2}$的图像的开口方向
(2)二次函数$y = -\frac{1}{2}x^{2}$的图像的开口方向
(1)二次函数$y = 2x^{2}$的图像的开口方向
向上
,对称轴是y轴
,顶点坐标是(0,0)
,$x$取任何实数时,对应的$y$值总是非负数
.(2)二次函数$y = -\frac{1}{2}x^{2}$的图像的开口方向
向下
,对称轴是y轴
,顶点坐标是(0,0)
,$x$取任何实数时,对应的$y$值总是非正数
.答案:(1)向上 y轴 (0,0) 非负数 (2)向下 y轴 (0,0) 非正数
3. 点$A(\frac{1}{2},b)$在二次函数$y = x^{2}$的图像上,则$b =$
$\frac{1}{4}$
;点$A$关于$y$轴的对称点$B$的坐标是$\left(-\frac{1}{2},\frac{1}{4}\right)$
,它在
(填“在”或“不在”)二次函数$y = x^{2}$的图像上;点$A$关于原点的对称点$C$的坐标是$\left(-\frac{1}{2},-\frac{1}{4}\right)$
,它不在
(填“在”或“不在”)二次函数$y = x^{2}$的图像上.答案:
$\frac {1}{4}$
$(-\frac {1}{2},$$\frac {1}{4})$
在
$(-\frac {1}{2},$$-\frac {1}{4})$
不在
$\frac {1}{4}$
$(-\frac {1}{2},$$\frac {1}{4})$
在
$(-\frac {1}{2},$$-\frac {1}{4})$
不在