活动一:画一画 想一想
如图 6 - 15,已知点$O$和$\triangle ABC$.
(1) 画射线$OA$、$OB$、$OC$,分别在$OA$、$OB$、$OC$上取点$A'$、$B'$、$C'$,使$\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}=2$,画$\triangle A'B'C'$;
(2) 分别在$OA$、$OB$、$OC$的反向延长线上取点$A''$、$B''$、$C''$,使$\frac{OA''}{OA}=\frac{OB''}{OB}=\frac{OC''}{OC}=\frac{1}{2}$,画$\triangle A''B''C''$.
(3) $\triangle A'B'C'$与$\triangle ABC$、$\triangle A''B''C''$与$\triangle ABC$是否相似?为什么?

如图 6 - 15,已知点$O$和$\triangle ABC$.
(1) 画射线$OA$、$OB$、$OC$,分别在$OA$、$OB$、$OC$上取点$A'$、$B'$、$C'$,使$\frac{OA'}{OA}=\frac{OB'}{OB}=\frac{OC'}{OC}=2$,画$\triangle A'B'C'$;
(2) 分别在$OA$、$OB$、$OC$的反向延长线上取点$A''$、$B''$、$C''$,使$\frac{OA''}{OA}=\frac{OB''}{OB}=\frac{OC''}{OC}=\frac{1}{2}$,画$\triangle A''B''C''$.
(3) $\triangle A'B'C'$与$\triangle ABC$、$\triangle A''B''C''$与$\triangle ABC$是否相似?为什么?

答案:
解:(1)如图所示
(2)如图所示
(3)△A'B'C'与△ABC、△A''B''C''与△ABC都相似,因为三边对应成比例
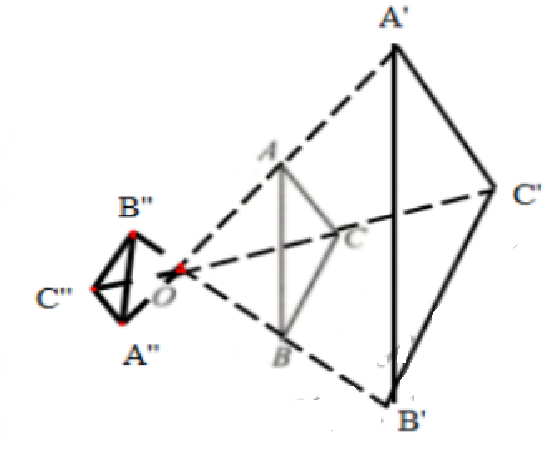
解:(1)如图所示
(2)如图所示
(3)△A'B'C'与△ABC、△A''B''C''与△ABC都相似,因为三边对应成比例

活动二:做一做 议一议
1. 结合画图过程,你认为位似图形具有哪些特征?与同学交流.
2. 完成课本“实践与探索”.
1. 结合画图过程,你认为位似图形具有哪些特征?与同学交流.
2. 完成课本“实践与探索”.
答案:解:位似图形首先是相似图形,并且两个相似多边形对应顶点的连线相交于一点,
对应边互相平行(或在同一条直线上)。
对应边互相平行(或在同一条直线上)。
1. 有下列说法:① 相似图形是位似图形;② 位似图形是相似图形;③ 位似图形中任意一对对应点到位似中心的距离之比等于位似比;④ 位似图形中的对应线段平行;⑤ 位似图形一定有位似中心.其中,正确的有(
A.1 个
B.2 个
C.3 个
D.4 个
C
).A.1 个
B.2 个
C.3 个
D.4 个
答案:C