活动三:想一想 写一写
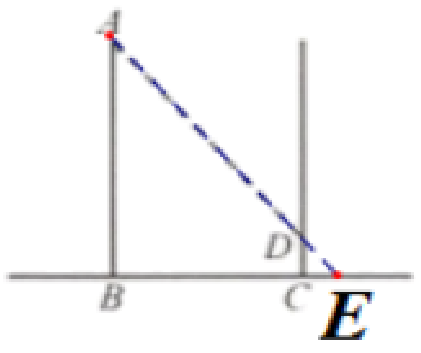
如图6-17,某兴趣小组利用投影的知识进行实地测量,其中一部分同学在某一时刻测得$1 m$长的竹竿影长是$0.9 m$,另一部分同学在同一时刻对大树$AB$的影长进行测量,但由于大树距离建筑物太近,树影没有完全落在地面上,有一部分树影落在建筑物的墙壁上,只测得地面上的树影长为$2.7 m$.
(1) 设树高为$y m$,树在墙上的影长为$x m$,写出$y$与$x$之间的函数表达式;
(2) 如果树高为$10 m$,那么此时留在墙壁上的树影有多高?

如图6-17,某兴趣小组利用投影的知识进行实地测量,其中一部分同学在某一时刻测得$1 m$长的竹竿影长是$0.9 m$,另一部分同学在同一时刻对大树$AB$的影长进行测量,但由于大树距离建筑物太近,树影没有完全落在地面上,有一部分树影落在建筑物的墙壁上,只测得地面上的树影长为$2.7 m$.
(1) 设树高为$y m$,树在墙上的影长为$x m$,写出$y$与$x$之间的函数表达式;
(2) 如果树高为$10 m$,那么此时留在墙壁上的树影有多高?

答案:
解: (1)延长AD与BC的延长线相交于点E
∴$\frac {CD}{CE}=\frac {AB}{BE}=\frac {1}{0.9}$
∴$\frac {x}{CE}=\frac {y}{2.7+CE}=\frac {10}{9}$
$CE=\frac {9x}{10}$
$y=\frac {10(2.7+CE)}{9}=x+3$
(2)由(1)可知y=x+3
当y=10时,x=7
答:此时留在墙壁上的树影高7m。
解: (1)延长AD与BC的延长线相交于点E
∴$\frac {CD}{CE}=\frac {AB}{BE}=\frac {1}{0.9}$
∴$\frac {x}{CE}=\frac {y}{2.7+CE}=\frac {10}{9}$
$CE=\frac {9x}{10}$
$y=\frac {10(2.7+CE)}{9}=x+3$
(2)由(1)可知y=x+3
当y=10时,x=7
答:此时留在墙壁上的树影高7m。

1. 已知$1.5 m$高的竹竿在阳光下的影长为$2.5 m$,那么同一时刻,在阳光下影长为$30 m$的旗杆的高为(
A.$15 m$
B.$16 m$
C.$18 m$
D.$20 m$
C
).A.$15 m$
B.$16 m$
C.$18 m$
D.$20 m$
答案:C
2. 如图,体育课上,甲、乙两名同学分别站在$C$、$D$的位置时,甲、乙两人影子的头部恰好重合在同一点$A$,已知甲、乙两名同学相距$1 m$,甲身高为$1.8 m$,乙身高为$1.5 m$,则甲的影长
是

是
6
$ m$.
答案:6
3. 如图,阳光从教室的窗户射入室内,窗户框$AB$在地面上的影长$DE=1.8 m$,窗户下沿到地
面的距离$BC = 1 m$,$EC = 1.2 m$,那么窗户的高$AB$为

面的距离$BC = 1 m$,$EC = 1.2 m$,那么窗户的高$AB$为
1.5
$ m$.
答案:1.5