活动一:算一算 填一填
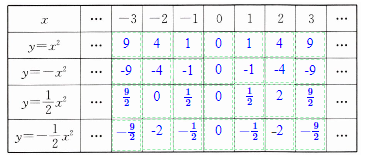
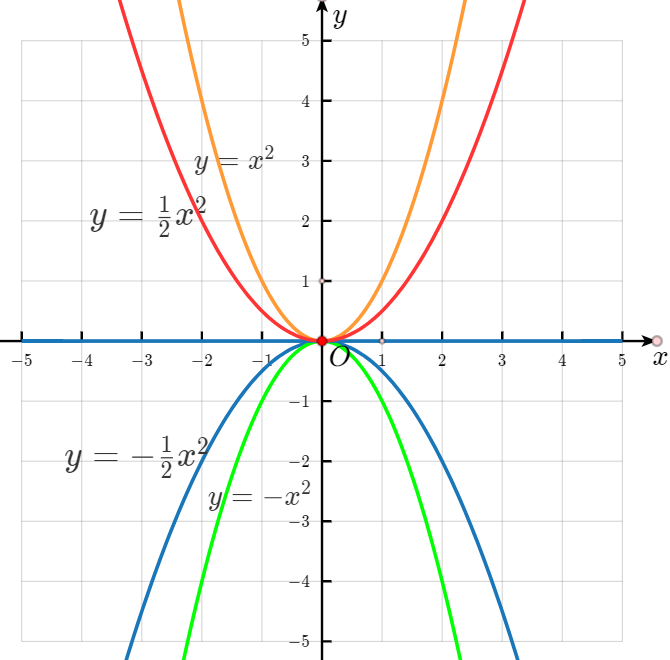
根据函数表达式填表,并在同一平面直角坐标系(图 5 - 2)中画出各函数的图像.


根据函数表达式填表,并在同一平面直角坐标系(图 5 - 2)中画出各函数的图像.


答案:


活动二:思一思 议一议
观察活动一中的表格和图像,尝试概括二次函数$y = x^{2}$、$y = \frac{1}{2}x^{2}$和$y = -\frac{1}{2}x^{2}$、$y = -x^{2}$的图像的相同点和不同点.
观察活动一中的表格和图像,尝试概括二次函数$y = x^{2}$、$y = \frac{1}{2}x^{2}$和$y = -\frac{1}{2}x^{2}$、$y = -x^{2}$的图像的相同点和不同点.
答案:解:共同点:4个函数图像的顶点都在原点,对称轴都是y轴.
不同点:二次函数y=x²,$y=\frac {1}{2}x²$的图像开口向上,顶点是抛物线的最低点;
二次函数y=-x²、$y=-\frac {1}{2}x²$的图像开口向下,顶点是抛物线的最高点
不同点:二次函数y=x²,$y=\frac {1}{2}x²$的图像开口向上,顶点是抛物线的最低点;
二次函数y=-x²、$y=-\frac {1}{2}x²$的图像开口向下,顶点是抛物线的最高点
活动三:比一比 写一写
二次函数$y = ax^{2}$的图像具有哪些特征?用数学语言描述$y = ax^{2}$的图像性质(提示:可以从抛物线的开口方向、顶点坐标、对称轴、函数值的变化趋势、函数的最值等来描述其特征).
二次函数$y = ax^{2}$的图像具有哪些特征?用数学语言描述$y = ax^{2}$的图像性质(提示:可以从抛物线的开口方向、顶点坐标、对称轴、函数值的变化趋势、函数的最值等来描述其特征).
答案:解:当$a\gt 0$时,抛物线开口方向向上,顶点坐标为(0,0),关于y轴对称,
函数在$x\lt 0$时,y随x的增大而减小,当$x\gt 0$时,y随x的增大而增大,
函数在x=0时,取最小值y=0。
当$a\lt 0$时,抛物线开口方向向下,顶点坐标为(0,0),关于y轴对称,
函数在$x\lt 0$时,y随x的增大而增大,当$x\gt 0$时,y随x的增大而减小,
函数在x=0时,取最大值y=0。
函数在$x\lt 0$时,y随x的增大而减小,当$x\gt 0$时,y随x的增大而增大,
函数在x=0时,取最小值y=0。
当$a\lt 0$时,抛物线开口方向向下,顶点坐标为(0,0),关于y轴对称,
函数在$x\lt 0$时,y随x的增大而增大,当$x\gt 0$时,y随x的增大而减小,
函数在x=0时,取最大值y=0。