活动一:操作思考
1. 观察一副三角尺:(1)它们有几个不同的锐角?分别是多少度?(2)每块三角尺的三边之间有怎样的数量关系?试用不同的方法进行表述.
2. (1)请根据三角尺的三边关系确定$\sin 30^{\circ}、\cos 30^{\circ}、\tan 30^{\circ}$的值.
(2)你还能求出一副三角尺中其他锐角的三角函数值吗?
1. 观察一副三角尺:(1)它们有几个不同的锐角?分别是多少度?(2)每块三角尺的三边之间有怎样的数量关系?试用不同的方法进行表述.
2. (1)请根据三角尺的三边关系确定$\sin 30^{\circ}、\cos 30^{\circ}、\tan 30^{\circ}$的值.
(2)你还能求出一副三角尺中其他锐角的三角函数值吗?
答案:解:一副三角尺有三个不同的锐角,它们分别是30°、45°、60°
三边关系是1: 1:$\sqrt{2}$或1 :$\sqrt{3}$:2
解:$sin 30°=\frac {1}{2};$$cos 30°=\frac {\sqrt{3}}{2};$$tan 30°=\frac {\sqrt{3}}{3}$
解:$sin 45°=cos 45°=\frac {\sqrt 2}{2};$tan 45°=1
三边关系是1: 1:$\sqrt{2}$或1 :$\sqrt{3}$:2
解:$sin 30°=\frac {1}{2};$$cos 30°=\frac {\sqrt{3}}{2};$$tan 30°=\frac {\sqrt{3}}{3}$
解:$sin 45°=cos 45°=\frac {\sqrt 2}{2};$tan 45°=1
活动二:归纳结论


答案:
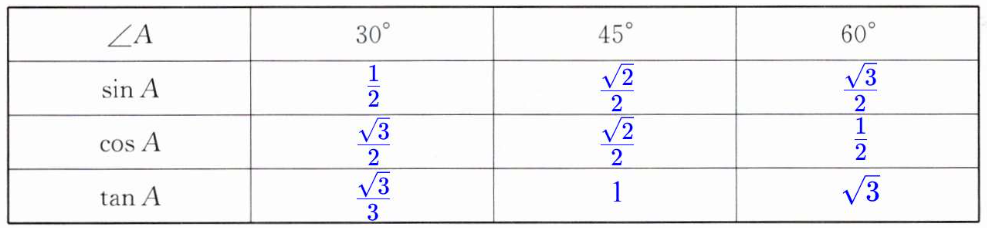

活动三:应用探索
利用特殊角的三角函数值,找出含特殊角的直角三角形的边角关系,并利用边角关系分别画出度数为$30^{\circ}、45^{\circ}、60^{\circ}$的角.
利用特殊角的三角函数值,找出含特殊角的直角三角形的边角关系,并利用边角关系分别画出度数为$30^{\circ}、45^{\circ}、60^{\circ}$的角.
答案:解:可以。
含30°的直角三角形的三边关系为1 :$\sqrt{3}$: 2
可以画出30°和60°的角
45°的直角三角形的三边关系为1 : 1 :$\sqrt{2}$
可以画出45°的角
含30°的直角三角形的三边关系为1 :$\sqrt{3}$: 2
可以画出30°和60°的角
45°的直角三角形的三边关系为1 : 1 :$\sqrt{2}$
可以画出45°的角
1. $\sin 60^{\circ}$的相反数是(
A.$-\frac{1}{2}$
B.$-\frac{\sqrt{3}}{3}$
C.$-\frac{\sqrt{3}}{2}$
D.$-\frac{\sqrt{2}}{2}$
C
).A.$-\frac{1}{2}$
B.$-\frac{\sqrt{3}}{3}$
C.$-\frac{\sqrt{3}}{2}$
D.$-\frac{\sqrt{2}}{2}$
答案:C
2. 已知$\alpha,\beta$是锐角,若$\sin\alpha=\frac{\sqrt{2}}{2},\cos\beta=\frac{\sqrt{2}}{2}$,则$\angle\alpha、\angle\beta$的大小关系是(
A.$\angle\alpha>\angle\beta$
B.$\angle\alpha<\angle\beta$
C.$\angle\alpha=\angle\beta$
D.$\angle\alpha = 2\angle\beta$
C
).A.$\angle\alpha>\angle\beta$
B.$\angle\alpha<\angle\beta$
C.$\angle\alpha=\angle\beta$
D.$\angle\alpha = 2\angle\beta$
答案:C