2. 一河堤横断面如图所示,堤高$BC = 5\ m$,迎水坡$AB$的坡度是$1 : \sqrt{3}$,则$AC$的长是(

A.$5\sqrt{3}\ m$
B.$10\ m$
C.$15\ m$
D.$10\sqrt{3}\ m$
(第 3 题)
A
).
A.$5\sqrt{3}\ m$
B.$10\ m$
C.$15\ m$
D.$10\sqrt{3}\ m$
(第 3 题)
答案:A
3. 如图,小明爬一个土坡,他从坡底$A$处爬到$B$处所走的距离$AB = 4\ m$,此时他离地面的高度$h = 2\ m$,则这个土坡的坡角$\angle A =$

30°
.
答案:30°
4. 为了做好防洪准备工作,某市在某常出现险情的河段修建了一防洪大坝. 如图,其横断面为四边形$ABCD$,已知$AB // CD$. 请你根据图中数据计算坝底$CD$的宽度(保留根号).


答案:解:∵∠C=45°
∴BE=CE=9m
∵∠D=60°
∴$DF=\frac {AF}{tan 60°}=3\sqrt{3}m$
∴$CD= DF+ EF+ EC= (19 + 3\sqrt{3})m$
答:坝底CD的宽度为$(19 + 3\sqrt{3})m。$
∴BE=CE=9m
∵∠D=60°
∴$DF=\frac {AF}{tan 60°}=3\sqrt{3}m$
∴$CD= DF+ EF+ EC= (19 + 3\sqrt{3})m$
答:坝底CD的宽度为$(19 + 3\sqrt{3})m。$
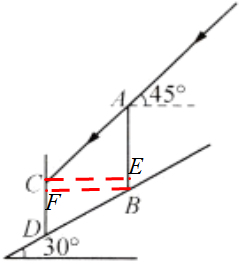
如图,在坡角为$30^{\circ}$的山坡上有一铁塔$AB$,其正前方矗立着一块大型广告牌,当阳光与水平线成$45^{\circ}$角时,测得铁塔$AB$落在斜坡上的影子$BD$的长为$6\ m$,落在广告牌上的影子$CD$的长为$4\ m$,求铁塔$AB$的高(保留根号).($AB$、$CD$均与水平面垂直)


答案:
解:过点C作CE⊥AB于E,过点B作BF⊥CD于F
∵在Rt△BFD中,∠DBF=30°
∴$sin∠DBF= \frac {DF}{BD}=\frac {1}{2}$
$cos∠DBF= \frac {BF}{BD}=\frac {\sqrt{3}}{2}$
∵BD=6
∴DF=3,$BF= 3\sqrt{3}$
∵AB//CD,CE⊥AB,BF⊥CD
∴四边形BFCE为矩形
∴$BF=CE= 3\sqrt{3},$CF=BE=CD-DF=1
∵在Rt△ACE中,∠ACE=45°
∴$AE=CE= 3\sqrt{3}$
∴$AB=AE+BE=3 \sqrt{3}+1$
即铁塔AB的高为$(3 \sqrt{3}+1)$米
解:过点C作CE⊥AB于E,过点B作BF⊥CD于F
∵在Rt△BFD中,∠DBF=30°
∴$sin∠DBF= \frac {DF}{BD}=\frac {1}{2}$
$cos∠DBF= \frac {BF}{BD}=\frac {\sqrt{3}}{2}$
∵BD=6
∴DF=3,$BF= 3\sqrt{3}$
∵AB//CD,CE⊥AB,BF⊥CD
∴四边形BFCE为矩形
∴$BF=CE= 3\sqrt{3},$CF=BE=CD-DF=1
∵在Rt△ACE中,∠ACE=45°
∴$AE=CE= 3\sqrt{3}$
∴$AB=AE+BE=3 \sqrt{3}+1$
即铁塔AB的高为$(3 \sqrt{3}+1)$米
