2. 如图,把一张矩形卡片 $ABCD$ 放在每格宽度为 $12 mm$ 的横格纸中,它的 4 个顶点恰好都在横格线上,已知 $\alpha = 36°$,求矩形卡片 $ABCD$ 的周长(精确到 $1 mm$;参考数据:$\sin 36° \approx 0.60$,$\cos 36° \approx 0.80$,$\tan 36° \approx 0.75$). 

答案:解:过点B作BE垂直于横格,过点D作DF 垂直于横格
由题意可知,$BE=24\ \mathrm {mm},$$DF=48\ \mathrm {mm}$
∵∠BAD=90°,
∴∠EAB+∠FAD=90°
∴∠EAB=∠ADF=36°
∴$AB=\frac {BE}{sin 36°}≈40\ \mathrm {mm},$$AD=\frac {DF}{cos 36°}≈60\ \mathrm {mm}$
$C_{矩形ABCD}=2(AB+ AD)= 200\ \mathrm {mm}$
答:矩形卡片△BCD的周长为$200\ \mathrm {mm}。$
由题意可知,$BE=24\ \mathrm {mm},$$DF=48\ \mathrm {mm}$
∵∠BAD=90°,
∴∠EAB+∠FAD=90°
∴∠EAB=∠ADF=36°
∴$AB=\frac {BE}{sin 36°}≈40\ \mathrm {mm},$$AD=\frac {DF}{cos 36°}≈60\ \mathrm {mm}$
$C_{矩形ABCD}=2(AB+ AD)= 200\ \mathrm {mm}$
答:矩形卡片△BCD的周长为$200\ \mathrm {mm}。$
3. 如图,某学校的大门是由相同的菱形框架组成的伸缩推拉门.已知大门关闭时菱形的边长为 $0.5 m$,锐角都是 $50°$,求大门的宽(精确到 $0.01 m$;参考数据:$\sin 25° \approx 0.4226$,$\cos 25° \approx 0.9063$). 

答案:
解:截取大门部分如图所示
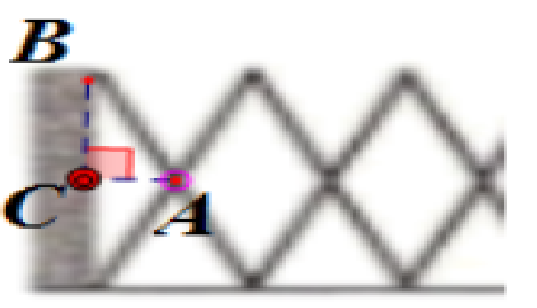
由题意可知,AB=0.5m
$∠ABC=\frac {1}{2}×50°=25°$
∴AC=sin 25°×AB≈0.211m
∴大门的宽d=9×2AC+ AC≈4.01m
答:大门的宽为4.01m。
解:截取大门部分如图所示

由题意可知,AB=0.5m
$∠ABC=\frac {1}{2}×50°=25°$
∴AC=sin 25°×AB≈0.211m
∴大门的宽d=9×2AC+ AC≈4.01m
答:大门的宽为4.01m。
1. 如图是某太阳能热水器的示意图,已知真空集热管 $AB$ 与支架 $CD$ 所在直线相交于水箱横断面$\odot O$ 的圆心,支架 $CD$ 与水平面 $AE$ 垂直,$AB = 150 cm$,$\angle BAC = 30°$,另一根辅助支架 $DE = 80 cm$,$\angle CED = 45°$.求热水器 $CF$ 的高度(保留根号). 

答案:解:∵∠CED=45°
∴$DC = sin 45°×DE = 40\sqrt{2}\ \mathrm {cm}$
设圆O的半径为r
∵∠BAC=30°,
∴OC=sin 30°×OA
∴$2(r+40\sqrt{2})=r+150,$
$r= 150 - 80\sqrt{2}$
$CF= CD+ 2r= (300- 120\sqrt{2})\ \mathrm {cm}$
答:热水器CF 的高度为$(300 - 120\sqrt{2})\ \mathrm {cm}。$
∴$DC = sin 45°×DE = 40\sqrt{2}\ \mathrm {cm}$
设圆O的半径为r
∵∠BAC=30°,
∴OC=sin 30°×OA
∴$2(r+40\sqrt{2})=r+150,$
$r= 150 - 80\sqrt{2}$
$CF= CD+ 2r= (300- 120\sqrt{2})\ \mathrm {cm}$
答:热水器CF 的高度为$(300 - 120\sqrt{2})\ \mathrm {cm}。$
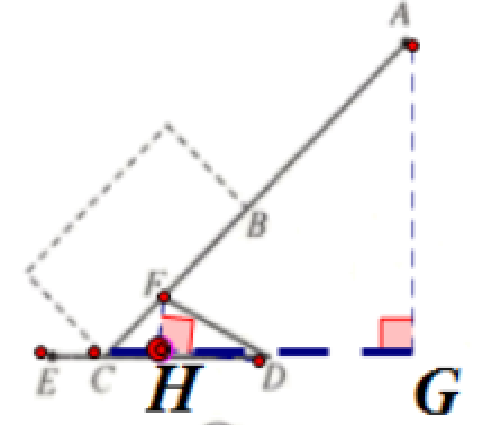
2. 如图是某种型号拉杆箱的实物图与示意图.根据商品介绍,可知如下信息:滑杆 $DE$、箱体 $BC$、拉杆 $AB$ 的长都相等,即 $DE = BC = AB$,点 $B$、$F$ 在 $AC$ 上,点 $C$ 在 $DE$ 上,支杆 $DF = 30 cm$,$CE : CD = 1 : 3$,$\angle DCF = 45°$,$\angle CDF = 30°$.
(1) 求 $AC$ 的长(保留根号);
(2) 求拉杆端点 $A$ 到水平滑杆 $DE$ 的距离(精确到 $1 cm$;参考数据:$\sqrt{2} \approx 1.41$,$\sqrt{3} \approx 1.73$,$\sqrt{6} \approx 2.45$).
(1) 求 $AC$ 的长(保留根号);
(2) 求拉杆端点 $A$ 到水平滑杆 $DE$ 的距离(精确到 $1 cm$;参考数据:$\sqrt{2} \approx 1.41$,$\sqrt{3} \approx 1.73$,$\sqrt{6} \approx 2.45$).

答案:
解: (1)过点F 作FH⊥CD交于点H
∵∠CDF=30°
∴$FH=DF×sin 30°=15\ \mathrm {cm},$
$DH=cos 30°×DF=15\sqrt{3}\ \mathrm {cm}$
∵∠DCF=45°
∴$CH=FH= 15\ \mathrm {cm}$
∴$CD= CH+ DH= (15 + 15\sqrt{3})\ \mathrm {cm}$
∵CE : CD= 1:3
∴$CE= (5+5\sqrt{3})\ \mathrm {cm}$
∴$DE= CE+CD= (20+20\sqrt{3})\ \mathrm {cm}$
∵DE= BC= AB
∴$AC= 2DE= (40 + 40\sqrt{3})\ \mathrm {cm}$
(2)过点A作AG⊥DE于点G
∵∠ACD=45°
∴$AG= sin 45°×AC= 20\sqrt{2}+20\sqrt{6}≈77\ \mathrm {cm}$
答:拉杆端点A到水平滑杆DE的距离是$77\ \mathrm {cm}。$
解: (1)过点F 作FH⊥CD交于点H
∵∠CDF=30°
∴$FH=DF×sin 30°=15\ \mathrm {cm},$
$DH=cos 30°×DF=15\sqrt{3}\ \mathrm {cm}$
∵∠DCF=45°
∴$CH=FH= 15\ \mathrm {cm}$
∴$CD= CH+ DH= (15 + 15\sqrt{3})\ \mathrm {cm}$
∵CE : CD= 1:3
∴$CE= (5+5\sqrt{3})\ \mathrm {cm}$
∴$DE= CE+CD= (20+20\sqrt{3})\ \mathrm {cm}$
∵DE= BC= AB
∴$AC= 2DE= (40 + 40\sqrt{3})\ \mathrm {cm}$
(2)过点A作AG⊥DE于点G
∵∠ACD=45°
∴$AG= sin 45°×AC= 20\sqrt{2}+20\sqrt{6}≈77\ \mathrm {cm}$
答:拉杆端点A到水平滑杆DE的距离是$77\ \mathrm {cm}。$
