活动一:测量深度
光从水进入空气中会发生折射.如图 7-14 所示是人看水中小鱼的光路图.此时,如果人看到水中的鱼距离水面约$30 cm$,那么这条鱼实际距离水面大约多少厘米(精确到$1 cm$;参考数据:$\tan48^{\circ}\approx1.11$,$\sqrt{3}\approx1.732$)?
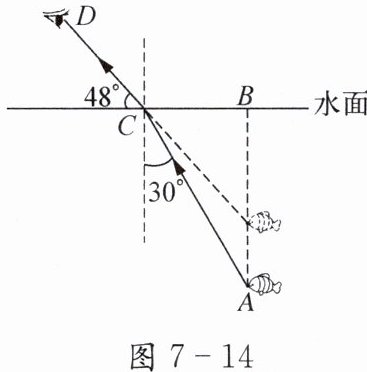
光从水进入空气中会发生折射.如图 7-14 所示是人看水中小鱼的光路图.此时,如果人看到水中的鱼距离水面约$30 cm$,那么这条鱼实际距离水面大约多少厘米(精确到$1 cm$;参考数据:$\tan48^{\circ}\approx1.11$,$\sqrt{3}\approx1.732$)?

答案:
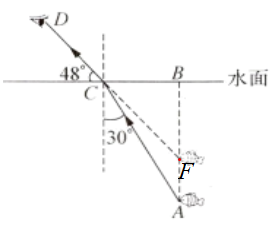
解:将人眼看到的水中的鱼的位置记为点F
在由题意可得$BF=30\ \mathrm {cm}$
由$tan 48°=\frac {BF}{BC},$可求得$BC=\frac {30}{tan 48°}≈27.03\ \mathrm {cm}$
由$tan 30°=\frac {BC}{AB},$可求得$AB=\frac {BC}{tan 30°}≈47\ \mathrm {cm}$
答:这条鱼实际距离水面大约47厘米。
解:将人眼看到的水中的鱼的位置记为点F
在由题意可得$BF=30\ \mathrm {cm}$
由$tan 48°=\frac {BF}{BC},$可求得$BC=\frac {30}{tan 48°}≈27.03\ \mathrm {cm}$
由$tan 30°=\frac {BC}{AB},$可求得$AB=\frac {BC}{tan 30°}≈47\ \mathrm {cm}$
答:这条鱼实际距离水面大约47厘米。

活动二:测量高度
数学活动课上,老师布置一项作业:请你任意选择一个无法直接测量高度的物体,并设计一个恰当的方法测量出它的高度.
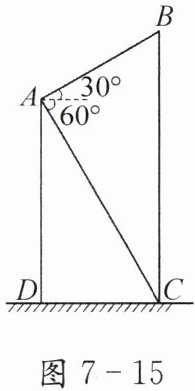
(1)如图 7-15,第一组同学选择测量操场上旗杆$BC$的高度,他们在教学楼上$A$处测得旗杆顶部$B$的仰角为$30^{\circ}$,旗杆底部$C$的俯角为$60^{\circ}$,已知点$A$距地面的高$AD$为$12 m$.
(2)如图 7-16,第二组同学选择测量一座古塔$CD$的高度.他们首先从$A$处测得塔顶$C$的仰角$\angle CFE = 21^{\circ}$,然后往塔的方向前进$50 m$到达$B$处,此时测得仰角$\angle CGE = 37^{\circ}$,已知测量仪器高$1.5 m$,请你根据以上数据计算出古塔$CD$的高度(参考数据:$\sin37^{\circ}\approx\frac{3}{5}$,$\tan37^{\circ}\approx\frac{3}{4}$,$\sin21^{\circ}\approx\frac{9}{25}$,$\tan21^{\circ}\approx\frac{3}{8}$).

(3)你还有其他测量学校旗杆高度的方法吗?若有,请写出你的方法.
数学活动课上,老师布置一项作业:请你任意选择一个无法直接测量高度的物体,并设计一个恰当的方法测量出它的高度.
(1)如图 7-15,第一组同学选择测量操场上旗杆$BC$的高度,他们在教学楼上$A$处测得旗杆顶部$B$的仰角为$30^{\circ}$,旗杆底部$C$的俯角为$60^{\circ}$,已知点$A$距地面的高$AD$为$12 m$.

(2)如图 7-16,第二组同学选择测量一座古塔$CD$的高度.他们首先从$A$处测得塔顶$C$的仰角$\angle CFE = 21^{\circ}$,然后往塔的方向前进$50 m$到达$B$处,此时测得仰角$\angle CGE = 37^{\circ}$,已知测量仪器高$1.5 m$,请你根据以上数据计算出古塔$CD$的高度(参考数据:$\sin37^{\circ}\approx\frac{3}{5}$,$\tan37^{\circ}\approx\frac{3}{4}$,$\sin21^{\circ}\approx\frac{9}{25}$,$\tan21^{\circ}\approx\frac{3}{8}$).

(3)你还有其他测量学校旗杆高度的方法吗?若有,请写出你的方法.
答案:
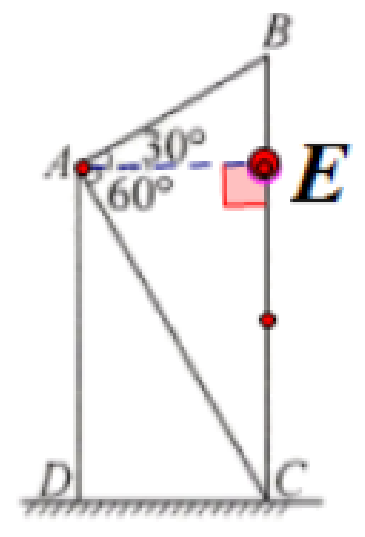
解:(1)过点A作AE⊥BC,垂足为E
CE=AD=12m
∵∠EAC= 60°
∴$AE=\frac {CE}{tan 60°}=4\sqrt{3}m$
∵∠BAE= 30°
∴BE=tan 30°×AE=4m
∴BC=BE+CE= 16m
解:(2)设GE= xcm
∵∠CGE=37°
∴$CE=GE×tan 37°≈\frac {3}{4}x$
∵∠CFE=21°
∴$EF=\frac {CE}{tan 21°}=2x$
∵EF= FG+GE=50+x
∴2x=50+x
x=50
∴$CE=\frac {3}{4}x= 37.5$
CD=CE+ED= 39m
答:古塔CD的高度约为39m。
解:在距旗杆底部5m 处,测得旗杆顶点B的仰角为60°。
则旗杆高度为$5×tan 60° =5\sqrt{3}m。$
解:(1)过点A作AE⊥BC,垂足为E
CE=AD=12m
∵∠EAC= 60°
∴$AE=\frac {CE}{tan 60°}=4\sqrt{3}m$
∵∠BAE= 30°
∴BE=tan 30°×AE=4m
∴BC=BE+CE= 16m

解:(2)设GE= xcm
∵∠CGE=37°
∴$CE=GE×tan 37°≈\frac {3}{4}x$
∵∠CFE=21°
∴$EF=\frac {CE}{tan 21°}=2x$
∵EF= FG+GE=50+x
∴2x=50+x
x=50
∴$CE=\frac {3}{4}x= 37.5$
CD=CE+ED= 39m
答:古塔CD的高度约为39m。
解:在距旗杆底部5m 处,测得旗杆顶点B的仰角为60°。
则旗杆高度为$5×tan 60° =5\sqrt{3}m。$