2. 锐角$A$满足$2\sin(A - 15^{\circ}) = \sqrt{3}$,则$\angle A =$
75
$^{\circ}$.答案:75
3. 如图,晾衣架由若干个菱形组成,已知其中每个菱形的边长为$20\ cm$,在墙上悬挂晾衣架的两个铁钉$A$、$B$之间的距离为$20\sqrt{3}\ cm$,则$\angle 1 =$

60
$^{\circ}$.
答案:60
4. 如图,在$\bigtriangleup ABC$中,$BD\perp AC$,垂足为$D$,$AB = 6$,$AC = 5\sqrt{3}$,$\angle A = 30^{\circ}$.
(1)求$BD$和$AD$的长;

(2)求$\tan C$的值.
(1)求$BD$和$AD$的长;

(2)求$\tan C$的值.
答案:解:$ (1)BD= sin 30°×AB=\frac {1}{2}×6=3$
$AD= cos 30°×AB=\frac {\sqrt{3}}{2}×6=3\sqrt{3}$
$(2)CD= AC-AD= 2\sqrt{3}$
$tan C=\frac {BD}{CD}=\frac {\sqrt{3}}{2}$
$AD= cos 30°×AB=\frac {\sqrt{3}}{2}×6=3\sqrt{3}$
$(2)CD= AC-AD= 2\sqrt{3}$
$tan C=\frac {BD}{CD}=\frac {\sqrt{3}}{2}$
1. 已知$\alpha$是锐角,且$\sin\alpha = 0.75$,则(
A.$0^{\circ}<\alpha<30^{\circ}$
B.$30^{\circ}<\alpha<45^{\circ}$
C.$45^{\circ}<\alpha<60^{\circ}$
D.$60^{\circ}<\alpha<90^{\circ}$
C
).A.$0^{\circ}<\alpha<30^{\circ}$
B.$30^{\circ}<\alpha<45^{\circ}$
C.$45^{\circ}<\alpha<60^{\circ}$
D.$60^{\circ}<\alpha<90^{\circ}$
答案:C
2. 比较大小:
(1)$\cos35^{\circ}$
(2)若$\sin\alpha = 0.3276$,$\sin\beta = 0.3274$,则$\alpha$
(1)$\cos35^{\circ}$
>
$\cos45^{\circ}$,$\tan50^{\circ}$<
$\tan60^{\circ}$;(2)若$\sin\alpha = 0.3276$,$\sin\beta = 0.3274$,则$\alpha$
>
$\beta$.答案:>
<
>
<
>
3. 如图,在$□ ABCD$中,对角线$AC$、$BD$相交成的锐角为$\alpha$,若$AC = a$,$BD = b$,则$□ ABCD$的面积是(

A.$\frac{1}{2}ab\sin\alpha$
B.$ab\sin\alpha$
C.$ab\cos\alpha$
D.$\frac{1}{2}ab\cos\alpha$
A
).
A.$\frac{1}{2}ab\sin\alpha$
B.$ab\sin\alpha$
C.$ab\cos\alpha$
D.$\frac{1}{2}ab\cos\alpha$
答案:A
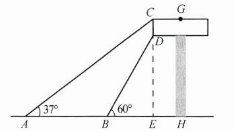
4. 一块广告牌的示意图如图所示. 已知$CD = 2\ m$,经测量,$\angle CAH = 37^{\circ}$,$\angle DBH = 60^{\circ}$,$AB = 10\ m$. 求广告牌的高度$GH$的长(结果精确到$0.1\ m$;参考数据:$\tan37^{\circ}\approx0.75$,$\sqrt{3}\approx1.732$).


答案:
解:延长CD,交AH于点E
根据题意得CE⊥AH
设DE=xm,则CE=(x+2)m
在Rt△AEC和Rt△BED中
$tan 37°=\frac {CE}{AE},$$tan 60°=\frac {DE}{BE},$
∴$AE=\frac {CE}{tan 37°},$$BE=\frac {DE}{tan 60°}$
∵AE-BE=AB
∴$\frac {CE}{tan 37°}-\frac {DE}{tan 60°}=10,$
即$\frac {x+2}{0.75}-\frac {x}{\sqrt{3}}=10$
解得x≈9.7
∴DE=9.7m
∴$GH=CE=CD+DE =2+9.7=11.7(\mathrm {m})$
解:延长CD,交AH于点E
根据题意得CE⊥AH
设DE=xm,则CE=(x+2)m
在Rt△AEC和Rt△BED中
$tan 37°=\frac {CE}{AE},$$tan 60°=\frac {DE}{BE},$
∴$AE=\frac {CE}{tan 37°},$$BE=\frac {DE}{tan 60°}$
∵AE-BE=AB
∴$\frac {CE}{tan 37°}-\frac {DE}{tan 60°}=10,$
即$\frac {x+2}{0.75}-\frac {x}{\sqrt{3}}=10$
解得x≈9.7
∴DE=9.7m
∴$GH=CE=CD+DE =2+9.7=11.7(\mathrm {m})$
