1.如图,某地修建一座高$BC = 5\ m$的天桥,已知天桥斜面$AB$的坡度为$1:\sqrt{3}$,则斜坡$AB$的长度为(

A.$10\ m$
B.$10\sqrt{3}\ m$
C.$5\ m$
D.$5\sqrt{3}\ m$
A
).
A.$10\ m$
B.$10\sqrt{3}\ m$
C.$5\ m$
D.$5\sqrt{3}\ m$
答案:A
2.如图,$AB$是半圆$O$的直径,点$C$在半圆上,过点$C$作$CD\perp AB$,垂足为$D$.已知$\cos\angle ACD=\frac{3}{5}$,$BC = 4$,则$AC$的长为(

A.$1$
B.$\frac{20}{3}$
C.$3$
D.$\frac{16}{3}$
D
).
A.$1$
B.$\frac{20}{3}$
C.$3$
D.$\frac{16}{3}$
答案:D
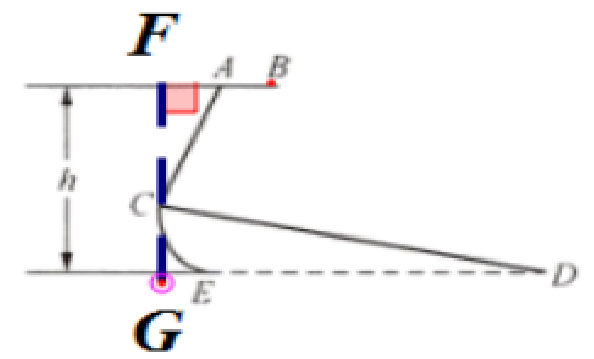
3.图①、图②分别是某种型号跑步机的实物图与示意图.已知踏板$CD$为$1.6\ m$,$CD$与地面$DE$的夹角$\angle CDE$为$12^{\circ}$,支架$AC$为$0.8\ m$,$\angle ACD$为$80^{\circ}$.求跑步机手柄的一端$A$的高度$h$.(结果精确到$0.1\ m$;参考数据:$\sin 12^{\circ}=\cos 78^{\circ}\approx 0.21$,$\sin 68^{\circ}=\cos 22^{\circ}\approx 0.93$,$\tan 68^{\circ}\approx 2.48$)


答案:
解:过点C作FG⊥AB,垂足为点F,交DE的延长线于点G
$CF= AC · sin∠CAF≈0.744\ \mathrm {m}$
在Rt△CDG 中
$CG = CD · sin∠CDE≈0.336\ \mathrm {m}$
则FG=FC+CG≈1.1m
答:跑步机手柄的一端A的高度约为$1.1\ \mathrm {m}。$
解:过点C作FG⊥AB,垂足为点F,交DE的延长线于点G
$CF= AC · sin∠CAF≈0.744\ \mathrm {m}$
在Rt△CDG 中
$CG = CD · sin∠CDE≈0.336\ \mathrm {m}$
则FG=FC+CG≈1.1m
答:跑步机手柄的一端A的高度约为$1.1\ \mathrm {m}。$
