10. 先用金属回形针做两个支架,分别与电池的两极连接;再用漆包线绕一个矩形线圈,线圈的两侧各留一段漆包线作为转轴;然后用小刀将一侧转轴上的漆皮全部刮去,将另一侧转轴上的漆皮只刮去半周;最后,把线圈放在支架上,并将蹄形磁体按图示的位置放置。闭合开关,轻推线圈,它就会持续转动起来。
(1)这个线圈能持续转动的原理和电动机一样吗?为什么?
(2)若要调节线圈转速,则应在电路中增加

(1)这个线圈能持续转动的原理和电动机一样吗?为什么?
(2)若要调节线圈转速,则应在电路中增加
滑动变阻器
(填写器材名称)。请在虚线框内画出电路图。
答案:
(1)一样;两者都是利用通电线圈在磁场中受力转动的原理制成,且通过特定装置(线圈转轴漆皮处理相当于电动机的换向器)改变线圈中电流方向(或切断电流利用惯性),使线圈持续转动。
(2)滑动变阻器;
电路图:
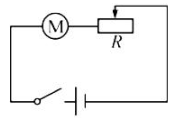
(1)一样;两者都是利用通电线圈在磁场中受力转动的原理制成,且通过特定装置(线圈转轴漆皮处理相当于电动机的换向器)改变线圈中电流方向(或切断电流利用惯性),使线圈持续转动。
(2)滑动变阻器;
电路图:

11. 一台交流电动机的线圈电阻为$12\ \Omega$,工作时通过线圈的电流是$5\ A$,加在它两端的电压是$220\ V$。在$5\ min$内,这台电动机所做的功和产生的热量分别是(
A.$3.3×10^{5}\ J$,$9×10^{4}\ J$
B.$1.5×10^{4}\ J$,$3.3×10^{5}\ J$
C.$3.3×10^{5}\ J$,$3.3×10^{3}\ J$
D.$1.5×10^{4}\ J$,$1.5×10^{4}\ J$
A
)。A.$3.3×10^{5}\ J$,$9×10^{4}\ J$
B.$1.5×10^{4}\ J$,$3.3×10^{5}\ J$
C.$3.3×10^{5}\ J$,$3.3×10^{3}\ J$
D.$1.5×10^{4}\ J$,$1.5×10^{4}\ J$
答案:A
解析:
电动机所做的功为电流对电动机所做的功,根据公式$W = UIt$,其中$U = 220\ V$,$I = 5\ A$,$t = 5 × 60 = 300\ s$,
计算得:$W = 220 × 5 × 300 = 330000\ J = 3.3 × 10^{5}\ J$;
电动机产生的热量为电流通过线圈电阻产生的热量,根据焦耳定律$Q = I^{2}Rt$,其中$I = 5\ A$,$R = 12\ \Omega$,$t = 300\ s$,
计算得:$Q = 5^{2} × 12 × 300 = 90000\ J = 9 × 10^{4}\ J$。
综上,电动机所做的功为$3.3 × 10^{5}\ J$,产生的热量为$9 × 10^{4}\ J$。
计算得:$W = 220 × 5 × 300 = 330000\ J = 3.3 × 10^{5}\ J$;
电动机产生的热量为电流通过线圈电阻产生的热量,根据焦耳定律$Q = I^{2}Rt$,其中$I = 5\ A$,$R = 12\ \Omega$,$t = 300\ s$,
计算得:$Q = 5^{2} × 12 × 300 = 90000\ J = 9 × 10^{4}\ J$。
综上,电动机所做的功为$3.3 × 10^{5}\ J$,产生的热量为$9 × 10^{4}\ J$。