1. 博物馆为展品准备了人工讲解、语音播报和 AR 增强三种讲解方式,博物馆共回收有效问卷 1000 张,其中 700 人没有讲解需求,剩余 300 人的需求情况如图所示(一人可以选择多种).在总共 2 万人的参观中,约有多少人需要 AR 增强讲解?


答案:解:(2)培训前平均分:
(25×2+5×6+2×8)÷32=3(分)
培训后平均分:
(8×2+16×6+8×8)÷32=5.5(分)
5.5-3=2.5(分)
(3)培训前良好的占比:16÷32=50\%
培训后良好的占比:8÷32=25\%
所以320×75\%=240(名)
$ 20000×\frac{100}{1000}=2000($人)
答:约有2000人需要AR增强讲解。
(25×2+5×6+2×8)÷32=3(分)
培训后平均分:
(8×2+16×6+8×8)÷32=5.5(分)
5.5-3=2.5(分)
(3)培训前良好的占比:16÷32=50\%
培训后良好的占比:8÷32=25\%
所以320×75\%=240(名)
$ 20000×\frac{100}{1000}=2000($人)
答:约有2000人需要AR增强讲解。
2. 某市九年级(1)班的一个研究性学习小组的研究课题是该市某高速公路入口的汽车流量问题.某天上午,他们在该入口处采用简单随机抽样的方法,对 3 min 内通过的汽车数量进行统计,得到如下数据:

试估计这天上午该入口处平均每小时通过多少辆汽车.

试估计这天上午该入口处平均每小时通过多少辆汽车.
答案:解: 3min内平均通过的汽车数量:
$\frac {49+50+64+58+53+56+55+47}{8}=54($辆)
估计平均每小时通过汽车数量: 54÷3×60=1080(辆)
答:估计这天上午该入口处平均每小时通过1080辆汽车。
$\frac {49+50+64+58+53+56+55+47}{8}=54($辆)
估计平均每小时通过汽车数量: 54÷3×60=1080(辆)
答:估计这天上午该入口处平均每小时通过1080辆汽车。
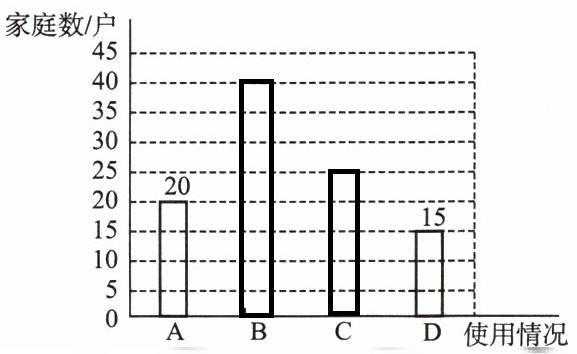
3. 学校环保调查小组就某小区每户家庭 1 周内环保塑料袋的使用情况进行了抽样调查,使用情况为 A(不使用)、B(1~3 个)、C(4~6 个)、D(7 个及以上),以下是根据调查结果绘制的统计图的一部分.

(1) 本次调查的样本容量是
(2) 已知该小区有 1500 户家庭,调查小组估计该小区 1 周内使用 7 个及以上环保塑料袋的家庭有 225 户.调查小组的估计是否合理? 请说明理由.

(1) 本次调查的样本容量是
100
,请补全条形统计图.(2) 已知该小区有 1500 户家庭,调查小组估计该小区 1 周内使用 7 个及以上环保塑料袋的家庭有 225 户.调查小组的估计是否合理? 请说明理由.
答案:
100
解:(2)合理,理由:
D所占比例为$\frac {15}{100}=15\%$
所以1500×15\%=225(户)
所以合理

100
解:(2)合理,理由:
D所占比例为$\frac {15}{100}=15\%$
所以1500×15\%=225(户)
所以合理