3. 某航班平均每次约有 a 名乘客,飞机失事的概率 $P = 0.000\ 05$,一家保险公司要为乘客提供保险,承诺飞机一旦失事,将向每位乘客赔偿人民币 60 万元. 平均来说,保险公司应该向每名乘客至少收取多少元保险费才不亏本?
答案:解:设收取x元保险费才不亏本.
ax=600000×0.00005×a
ax=30a
x=30
答:至少收取30元保险费才不亏本.
ax=600000×0.00005×a
ax=30a
x=30
答:至少收取30元保险费才不亏本.
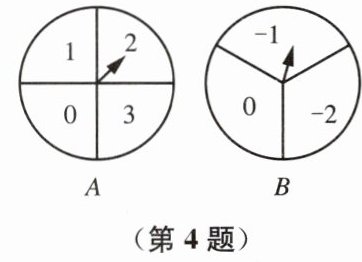
4. 如图,有两个可以自由转动的转盘 A、B 分别被分成 4 等份、3 等份,每份内均标有数字.小明和小丽用这两个转盘做游戏,游戏规则如下:
① 分别转动转盘 A 与 B.
② 两个转盘停止后,将两个指针所指的数字相加.
③ 如果和为 0,则小明获胜;否则小丽获胜.
(1)请用“列表”或“画树状图”的方法,求小明获胜的概率.
(2)你认为这个游戏对双方公平吗?若不公平,请制订一个新的游戏规则.
① 分别转动转盘 A 与 B.
② 两个转盘停止后,将两个指针所指的数字相加.
③ 如果和为 0,则小明获胜;否则小丽获胜.
(1)请用“列表”或“画树状图”的方法,求小明获胜的概率.
(2)你认为这个游戏对双方公平吗?若不公平,请制订一个新的游戏规则.

答案:4.(1) $\frac{1}{4}$;(2) 不公平,把“否则小丽获胜”改为“如果和为1,小丽获胜”,其余规则不变(答案不唯一).
解析:
(1) 列表如下:
| 转盘A\转盘B | -1 | 0 | -2 |
| --- | --- | --- | --- |
| 1 | 0 | 1 | -1 |
| 2 | 1 | 2 | 0 |
| 0 | -1 | 0 | -2 |
| 3 | 2 | 3 | 1 |
共有12种等可能的结果,其中和为0的有3种,所以小明获胜的概率为$\frac{3}{12}=\frac{1}{4}$。
(2) 不公平。新规则:如果和为1,则小丽获胜,其余规则不变(答案不唯一)。
| 转盘A\转盘B | -1 | 0 | -2 |
| --- | --- | --- | --- |
| 1 | 0 | 1 | -1 |
| 2 | 1 | 2 | 0 |
| 0 | -1 | 0 | -2 |
| 3 | 2 | 3 | 1 |
共有12种等可能的结果,其中和为0的有3种,所以小明获胜的概率为$\frac{3}{12}=\frac{1}{4}$。
(2) 不公平。新规则:如果和为1,则小丽获胜,其余规则不变(答案不唯一)。
5. 某节日晚会的游戏环节设置了“猜猜看”游戏,规则如下:每道题目有 4 个选项,其中有 2 个正确答案,选出 2 个正确答案且没有多选任何一个错误答案得 2 分,选出一个正确答案且没有多选任何一个错误答案得 1 分,不选或所选答案中至少有一个错误答案得 0 分.
(1)任选 2 个答案,请用“画树状图”或“列表”的方法,求得 2 分的概率;
(2)如果只能确认 4 个选项中的某一个答案是正确的,写出此时的最佳答题策略,并说明理由.
(1)任选 2 个答案,请用“画树状图”或“列表”的方法,求得 2 分的概率;
(2)如果只能确认 4 个选项中的某一个答案是正确的,写出此时的最佳答题策略,并说明理由.
答案:
解:(1)画树状图如下
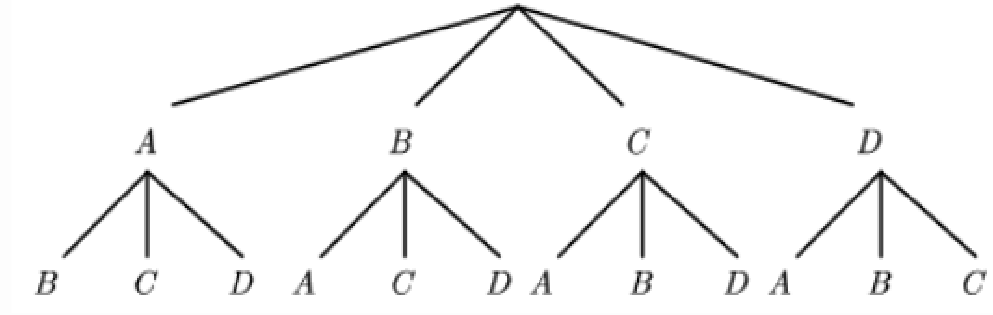
一共有12种等可能结果,得2分的有2种
所以P(得2分$)=\frac {2}{12}=\frac {1}{6}$
(2)如果选择正确的那个选项后,再随机选择一项,
那么有3种等可能的结果,其中得0分的有2种,得2分的有1种,
P(得0分$)=\frac {2}{3},$ P(得2分$)=\frac {1}{3} ,$
加权平均分为$0×\frac {2}{3}+2×\frac {1}{3}=\frac {2}{3}($分) ;
如果只选择正确的那个选项,得1分;
$\frac {2}{3}$分$\lt 1$分
所以最佳答题策略是只选择那一个正确的选项
解:(1)画树状图如下

一共有12种等可能结果,得2分的有2种
所以P(得2分$)=\frac {2}{12}=\frac {1}{6}$
(2)如果选择正确的那个选项后,再随机选择一项,
那么有3种等可能的结果,其中得0分的有2种,得2分的有1种,
P(得0分$)=\frac {2}{3},$ P(得2分$)=\frac {1}{3} ,$
加权平均分为$0×\frac {2}{3}+2×\frac {1}{3}=\frac {2}{3}($分) ;
如果只选择正确的那个选项,得1分;
$\frac {2}{3}$分$\lt 1$分
所以最佳答题策略是只选择那一个正确的选项