2. 下列关于二次函数 $ y = 2x^{2}-3x + 4 $ 的判断中正确的是 (
A.$ y $ 的最大值为 $ \frac{23}{8} $
B.$ y $ 的最小值为 $ \frac{23}{8} $
C.函数图像的对称轴为 $ y $ 轴所在的直线
D.以上都不正确
B
)A.$ y $ 的最大值为 $ \frac{23}{8} $
B.$ y $ 的最小值为 $ \frac{23}{8} $
C.函数图像的对称轴为 $ y $ 轴所在的直线
D.以上都不正确
答案:B
3. 对于二次函数 $ y = x^{2}+2x - 3 $,当 $ x $
$> -1$
时,$ y $ 随 $ x $ 的增大而增大.答案:>-1
4. 若二次函数 $ y = ax^{2}-4x - 6 $ 的图像的顶点的横坐标是 $ - 2 $,则 $ a $ 的值为
$-1$
.答案:-1
三、解答题
5. 已知二次函数 $ y = ax^{2}-2x + c $ 的图像的顶点坐标是 $ (1,-1) $,求 $ a $、$ c $ 的值.
5. 已知二次函数 $ y = ax^{2}-2x + c $ 的图像的顶点坐标是 $ (1,-1) $,求 $ a $、$ c $ 的值.
答案:解:由题意可得:
$\begin{cases}{ -\dfrac {-2}{2a}=1}\\{a-2+c=-1} \end{cases}$
解得a=1,c=0
$\begin{cases}{ -\dfrac {-2}{2a}=1}\\{a-2+c=-1} \end{cases}$
解得a=1,c=0
6. 先利用配方法求出二次函数 $ y = 2x^{2}-4x - 1 $ 的图像的顶点坐标、对称轴、最大值或最小值,然后在平面直角坐标系中画出这个函数的图像.
答案:
解:y=2x²-4x-1=2(x²-2x)-1=2(x-1)²-3
所以顶点坐标为(1,-3) ,对称轴是x =1,y的最小值是-3
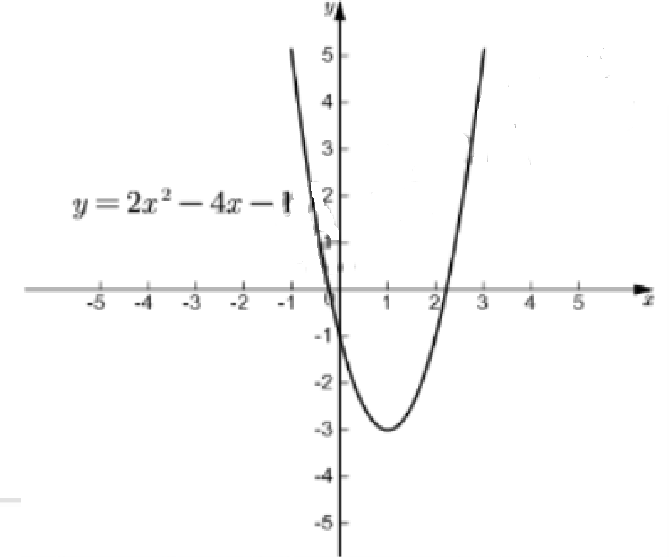
解:y=2x²-4x-1=2(x²-2x)-1=2(x-1)²-3
所以顶点坐标为(1,-3) ,对称轴是x =1,y的最小值是-3

7. 若二次函数 $ y = ax^{2}+bx + c(a\neq0) $ 的图像经过点 $ A(1,0) $、$ B(3,0) $,则这个函数图像的对称轴为
过点$(2,0)$且平行于$y$轴的直线
.答案:过点(2,0)且平行于y轴的直线
8. 已知二次函数 $ y = x^{2}+4x + c $ 的图像的顶点 $ P $ 在一次函数 $ y = 3x + 5 $ 的图像上.
(1) 求 $ c $ 的值,并求顶点 $ P $ 的坐标.
(2) 除点 $ P $ 外,这两个函数的图像是否还存在其他公共点? 若存在,请求出它的坐标;若不存在,请说明理由.
(1) 求 $ c $ 的值,并求顶点 $ P $ 的坐标.
(2) 除点 $ P $ 外,这两个函数的图像是否还存在其他公共点? 若存在,请求出它的坐标;若不存在,请说明理由.
答案:解:(1)y=x²+ 4x+c
= (x+2)²+c-4
所以二次函数y= x²+4x+ c的顶点P的坐标为(-2 , c-4)
因为P(-2 , c- 4)在一次函数y= 3x+ 5的图像上
所以c- 4= 3×(-2)+ 5
所以c= 3
所以顶点P的坐标为(-2 , -1)
(2)存在,
由题意得,
x²+4x+3= 3x+5
解得,${x}_1=-2 ,$$ {x}_2= 1$
将x= 1代入y=3x+5,得y=3+5=8
另一个公共点的坐标为(1 , 8)
= (x+2)²+c-4
所以二次函数y= x²+4x+ c的顶点P的坐标为(-2 , c-4)
因为P(-2 , c- 4)在一次函数y= 3x+ 5的图像上
所以c- 4= 3×(-2)+ 5
所以c= 3
所以顶点P的坐标为(-2 , -1)
(2)存在,
由题意得,
x²+4x+3= 3x+5
解得,${x}_1=-2 ,$$ {x}_2= 1$
将x= 1代入y=3x+5,得y=3+5=8
另一个公共点的坐标为(1 , 8)