例 1 根据下列条件,分别求出二次函数的表达式.
(1)已知二次函数图像的顶点坐标为$(1,-3)$,且与$y$轴相交于点$(0,1)$;
(2)已知二次函数图像与$x$轴交于点$(-3,0)$、$(5,0)$,且与$y$轴相交于点$(0,-3)$;
(3)已知二次函数图像的顶点坐标为$(3,-2)$,且与$x$轴的两个公共点间的距离为 4.
(1)已知二次函数图像的顶点坐标为$(1,-3)$,且与$y$轴相交于点$(0,1)$;
(2)已知二次函数图像与$x$轴交于点$(-3,0)$、$(5,0)$,且与$y$轴相交于点$(0,-3)$;
(3)已知二次函数图像的顶点坐标为$(3,-2)$,且与$x$轴的两个公共点间的距离为 4.
答案:解:(1)设y=a(x-1)²-3,
把(0, 1)代入得a= 4,
所以y= 4x²- 8x+ 1
(2)设y=a(x + 3)(x-5)= ax²- 2ax-15a
所以- 15a=-3,
所以$a=\frac {1}{5}$
所以$y=\frac {1}{5}x²-\frac {2}{5}x-3$
(3)两公共点分别为(1 , 0),(5, 0)
设y=a(x-3)²-2 ,
把(1 , 0)代入得$a =\frac {1}{2}$
所以$y=\frac {1}{2}x²- 3x+\frac {5}{2}$
把(0, 1)代入得a= 4,
所以y= 4x²- 8x+ 1
(2)设y=a(x + 3)(x-5)= ax²- 2ax-15a
所以- 15a=-3,
所以$a=\frac {1}{5}$
所以$y=\frac {1}{5}x²-\frac {2}{5}x-3$
(3)两公共点分别为(1 , 0),(5, 0)
设y=a(x-3)²-2 ,
把(1 , 0)代入得$a =\frac {1}{2}$
所以$y=\frac {1}{2}x²- 3x+\frac {5}{2}$
例 2 已知二次函数图像的对称轴经过点$(1,0)$且平行于$y$轴,它与$x$轴相交于$A$、$B$两点,与$y$轴相交于点$C$,点$A$、$C$的坐标分别是$(-1,0)$、$(0,\frac{3}{2})$.
(1)请在图 5.3.1 所给的平面直角坐标系中画出示意图;
(2)求此图像相应的函数表达式;
(3)若$P$是此二次函数图像上位于$x$轴上方的一个动点,求$\triangle ABP$面积的最大值.

(1)请在图 5.3.1 所给的平面直角坐标系中画出示意图;
(2)求此图像相应的函数表达式;
(3)若$P$是此二次函数图像上位于$x$轴上方的一个动点,求$\triangle ABP$面积的最大值.

答案:
解:(1)
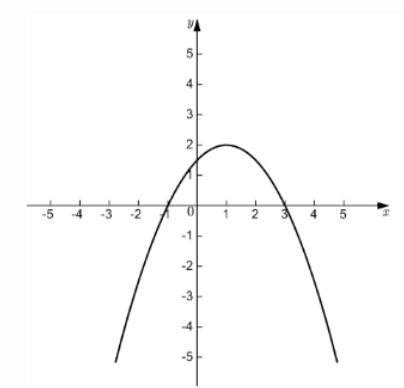
(2)设函数表达式为y= ax²+ bx+c
由题意得,$\begin{cases}{-\dfrac {b}{2a}=1 }\\{a-b+c=0}\\{\dfrac {3}{2}=c} \end{cases}$
解得$a=-\frac {1}{2},$b=1,$c=\frac {3}{2}$
所以此图像相应的函数表达式为$y=-\frac {1}{2}x²+x+\frac {3}{2}$
(3)令y= 0,得$0= -\frac {1}{2}x²+x+\frac {3}{2}$
解得,${x}_1=-1,$${x}_2=3$
所以点B坐标为(3 , 0)
所以AB=4
设点P{坐标} 为(t,$-\frac {1}{2}t²+t+\frac {3}{2})$
所以$S_{△ABP}=\frac {1}{2}×4×(-\frac {1}{2}t²+t+\frac {3}{2})$
=-t²+2t+3
=-(t-1)²+4
因为点P 在x轴上方
所以-1<t<5
当t = 1时, △ABP的面积最大 ,最大值为4
解:(1)

(2)设函数表达式为y= ax²+ bx+c
由题意得,$\begin{cases}{-\dfrac {b}{2a}=1 }\\{a-b+c=0}\\{\dfrac {3}{2}=c} \end{cases}$
解得$a=-\frac {1}{2},$b=1,$c=\frac {3}{2}$
所以此图像相应的函数表达式为$y=-\frac {1}{2}x²+x+\frac {3}{2}$
(3)令y= 0,得$0= -\frac {1}{2}x²+x+\frac {3}{2}$
解得,${x}_1=-1,$${x}_2=3$
所以点B坐标为(3 , 0)
所以AB=4
设点P{坐标} 为(t,$-\frac {1}{2}t²+t+\frac {3}{2})$
所以$S_{△ABP}=\frac {1}{2}×4×(-\frac {1}{2}t²+t+\frac {3}{2})$
=-t²+2t+3
=-(t-1)²+4
因为点P 在x轴上方
所以-1<t<5
当t = 1时, △ABP的面积最大 ,最大值为4