17. (10分)如图,点$P$在$\triangle ABC$的内部,点$F$、$D$在$AB$上,点$E$、$I$在$AC$上,点$H$、$G$在$BC$上,$FG // AC$,$HI // AB$,$DE // BC$,且$\triangle FDP$、$\triangle IPE$、$\triangle PHG$的面积分别为$4$、$9$和$49$.求$\triangle ABC$的面积.
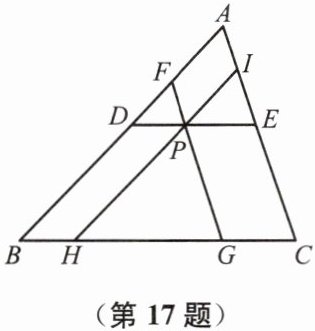

答案:解: 因为FG//AC , HI//AB
所以∠FPD=∠IEP,∠FDP=∠IPE
所以△FDP∽△IPE
因为△FDP、△IPE的面积分别为4、 9
所以$\frac {S_{△FDP}}{S_{△IPE}}=(\frac {DP}{PE})²=\frac {4}{9}$
所以$\frac {DP}{PE}=\frac {2}{3}$
同理可得,$\frac {FP}{PG}=\frac {2}{7}$
设DP=2x ,则PE=3x .
因为DP//BC , HI//AB
所以∠FPD=∠PGH ,∠DFP=∠HPG ,
所以△FDP∽△PHG
所以$\frac {DP}{HG}=\frac {FP}{PG}=\frac {2}{7}$
因为DP=2x,
所以HG=7x
因为FG//AC , HI//AB , DE//BC
所以四边形DPHB和四边形PECG都为平行四边形
所以BH=DP=2x,CG=PE=3x,
所以BC=BH+HG+CG=12x
因为DE//BC,FG//AC,
所以∠FDP=∠B ,∠DFP=∠A
所以△FDP∽△ABC
所以$\frac {S_{△FDP}}{S_{△ABC}}=(\frac {DP}{BC})²=(\frac {2x}{12x})²=\frac {1}{36}$
因为$S_{△FDP}=4 ,$
所以$S_{△ABC}= 144$
所以∠FPD=∠IEP,∠FDP=∠IPE
所以△FDP∽△IPE
因为△FDP、△IPE的面积分别为4、 9
所以$\frac {S_{△FDP}}{S_{△IPE}}=(\frac {DP}{PE})²=\frac {4}{9}$
所以$\frac {DP}{PE}=\frac {2}{3}$
同理可得,$\frac {FP}{PG}=\frac {2}{7}$
设DP=2x ,则PE=3x .
因为DP//BC , HI//AB
所以∠FPD=∠PGH ,∠DFP=∠HPG ,
所以△FDP∽△PHG
所以$\frac {DP}{HG}=\frac {FP}{PG}=\frac {2}{7}$
因为DP=2x,
所以HG=7x
因为FG//AC , HI//AB , DE//BC
所以四边形DPHB和四边形PECG都为平行四边形
所以BH=DP=2x,CG=PE=3x,
所以BC=BH+HG+CG=12x
因为DE//BC,FG//AC,
所以∠FDP=∠B ,∠DFP=∠A
所以△FDP∽△ABC
所以$\frac {S_{△FDP}}{S_{△ABC}}=(\frac {DP}{BC})²=(\frac {2x}{12x})²=\frac {1}{36}$
因为$S_{△FDP}=4 ,$
所以$S_{△ABC}= 144$
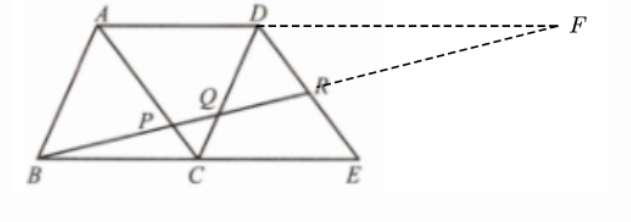
18. (12分)如图,四边形$ABCD$和四边形$ACED$都是平行四边形,$R$是$DE$的中点,$BR$分别交$AC$、$CD$于点$P$、$Q$.
(1)请写出图中的相似三角形(相似比不为1);
(2)求$BP:PQ:QR$.

(1)请写出图中的相似三角形(相似比不为1);
(2)求$BP:PQ:QR$.

答案:
解:(1)△ABP∽△CQP∽△DQR,△BPC∽△BRE
(2)延长AD、$BR_{交于}F$
由平行四边形A BCD和平行四边形ACED
得AD//BC , AB//CD, AC//DE , AD= BC= CE,
所以$\frac {FR}{BR}=\frac {DF}{BE}=\frac {DR}{RE}=1,$DF=BE,
$\frac {QF}{BQ}=\frac {DF}{BC}=2$
$\frac {PF}{BP}=\frac {AF}{BC}=3$
即BP: (BP+ PQ+ PR): (BP+ 2PQ+ 2PR)=1 : 2: 3
设BP=x,则x+PQ+PR=2x,x+2PQ+PR=3x
得$PQ=\frac {1}{3}x,$$PR=\frac {2}{3}x$
所以BP: PQ : QR=3:1: 2
解:(1)△ABP∽△CQP∽△DQR,△BPC∽△BRE
(2)延长AD、$BR_{交于}F$
由平行四边形A BCD和平行四边形ACED
得AD//BC , AB//CD, AC//DE , AD= BC= CE,
所以$\frac {FR}{BR}=\frac {DF}{BE}=\frac {DR}{RE}=1,$DF=BE,
$\frac {QF}{BQ}=\frac {DF}{BC}=2$
$\frac {PF}{BP}=\frac {AF}{BC}=3$
即BP: (BP+ PQ+ PR): (BP+ 2PQ+ 2PR)=1 : 2: 3
设BP=x,则x+PQ+PR=2x,x+2PQ+PR=3x
得$PQ=\frac {1}{3}x,$$PR=\frac {2}{3}x$
所以BP: PQ : QR=3:1: 2
