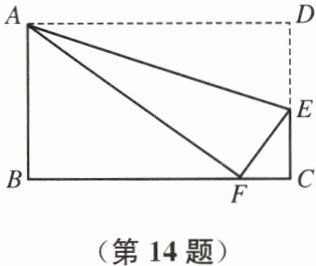
14. (8分)如图,将矩形纸片$ABCD$沿$AE$折叠,使点$D$落在边$BC$上的点$F$处.已知$AB = 3\ \mathrm{cm}$,$AD = 5\ \mathrm{cm}$,求$DE$的长.

答案:$14.\frac{5}{3}$
解析:
解:
∵四边形$ABCD$是矩形,
$\therefore AB=CD=3\ \mathrm{cm}$,$AD=BC=5\ \mathrm{cm}$,$\angle B=\angle C=\angle D=90°$。
由折叠性质得:$AF=AD=5\ \mathrm{cm}$,$EF=DE$。
设$DE=EF=x\ \mathrm{cm}$,则$EC=(3 - x)\ \mathrm{cm}$。
在$\mathrm{Rt}\triangle ABF$中,$BF=\sqrt{AF^2 - AB^2}=\sqrt{5^2 - 3^2}=4\ \mathrm{cm}$,
$\therefore CF=BC - BF=5 - 4=1\ \mathrm{cm}$。
在$\mathrm{Rt}\triangle ECF$中,$EF^2=EC^2 + CF^2$,
即$x^2=(3 - x)^2 + 1^2$,
解得$x=\frac{5}{3}$。
$\therefore DE$的长为$\frac{5}{3}\ \mathrm{cm}$。
∵四边形$ABCD$是矩形,
$\therefore AB=CD=3\ \mathrm{cm}$,$AD=BC=5\ \mathrm{cm}$,$\angle B=\angle C=\angle D=90°$。
由折叠性质得:$AF=AD=5\ \mathrm{cm}$,$EF=DE$。
设$DE=EF=x\ \mathrm{cm}$,则$EC=(3 - x)\ \mathrm{cm}$。
在$\mathrm{Rt}\triangle ABF$中,$BF=\sqrt{AF^2 - AB^2}=\sqrt{5^2 - 3^2}=4\ \mathrm{cm}$,
$\therefore CF=BC - BF=5 - 4=1\ \mathrm{cm}$。
在$\mathrm{Rt}\triangle ECF$中,$EF^2=EC^2 + CF^2$,
即$x^2=(3 - x)^2 + 1^2$,
解得$x=\frac{5}{3}$。
$\therefore DE$的长为$\frac{5}{3}\ \mathrm{cm}$。
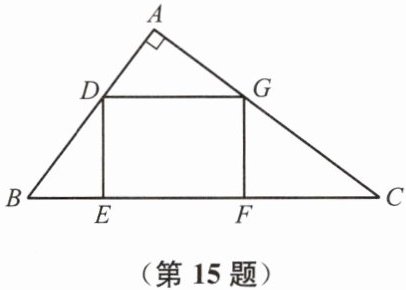
15. (8分)如图,在$\triangle ABC$中,$\angle A = 90^{\circ}$,$AB = 12\ \mathrm{cm}$,$AC = 16\ \mathrm{cm}$,矩形$DEFG$的顶点都在$\triangle ABC$的边上,且$DE:EF = 3:5$.求矩形$DEFG$的周长.

答案:
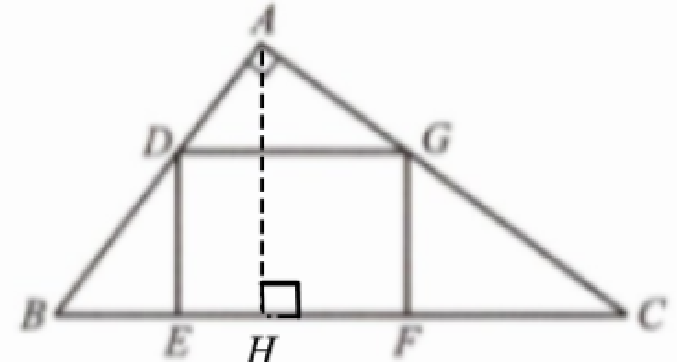
解:作AH⊥BC于H,
则AH//DE,DG//BC
所以$\frac {DE}{AH}=\frac {BD}{AB}=1-\frac {AD}{AB}=1-\frac {DG}{BC}$
$BC=\sqrt{12²+16²}=20\ \mathrm {cm},$$AH=\frac {12×16}{20}=\frac {48}{5}\ \mathrm {cm}$
设$DE= 3x\ \mathrm {cm},$
则$DG= EF = 5x\ \mathrm {cm}$
所以$\frac {3x}{\frac {48}{5}}=1-\frac {5x}{20}$
解得$x=\frac {16}{9}$
所以矩形DEFG的周长$= 2(DE+ DG)= 16x= \frac {256}{9}\ \mathrm {cm} .$
解:作AH⊥BC于H,
则AH//DE,DG//BC
所以$\frac {DE}{AH}=\frac {BD}{AB}=1-\frac {AD}{AB}=1-\frac {DG}{BC}$
$BC=\sqrt{12²+16²}=20\ \mathrm {cm},$$AH=\frac {12×16}{20}=\frac {48}{5}\ \mathrm {cm}$
设$DE= 3x\ \mathrm {cm},$
则$DG= EF = 5x\ \mathrm {cm}$
所以$\frac {3x}{\frac {48}{5}}=1-\frac {5x}{20}$
解得$x=\frac {16}{9}$
所以矩形DEFG的周长$= 2(DE+ DG)= 16x= \frac {256}{9}\ \mathrm {cm} .$

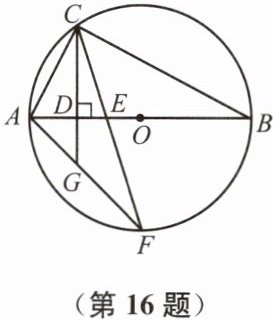
16. (9分)已知:如图,$AB$是$\odot O$的直径,点$C$在$\odot O$上,$CD ⊥ AB$,垂足为$D$,弦$CF$交$AB$于点$E$,$CD$的延长线交$AF$于点$G$.
求证:(1)$\angle ACD = \angle F$;(2)$AC^{2} = AG · AF$.
求证:(1)$\angle ACD = \angle F$;(2)$AC^{2} = AG · AF$.

答案:证明: (1)因为AB是○O的直径
所以∠ACB =90°
所以∠CAB+∠B=90°
因为CD⊥AB
所以∠CDA= 90°
所以∠CAB+∠ACD=90°
所以∠B=∠ACD
因为∠B=∠F
所以∠ACD=∠F
(2)因为∠ACD=∠F ,∠CAG=∠CAF
所以△ACG∽△AFC
所以$\frac {AC}{AF}=\frac {AG}{AC}$
所以AC²= AG×AF
所以∠ACB =90°
所以∠CAB+∠B=90°
因为CD⊥AB
所以∠CDA= 90°
所以∠CAB+∠ACD=90°
所以∠B=∠ACD
因为∠B=∠F
所以∠ACD=∠F
(2)因为∠ACD=∠F ,∠CAG=∠CAF
所以△ACG∽△AFC
所以$\frac {AC}{AF}=\frac {AG}{AC}$
所以AC²= AG×AF