14. 一个不透明的盒子里装有4张书签,分别描绘"春""夏""秋""冬"四个季节,书签除图案外都相同,将4张书签充分搅匀.
(1)若从盒子中任意抽取1张书签,恰好抽到"夏"的概率为
(2)若从盒子中任意抽取2张书签,求抽取的书签恰好1张为"春"、1张为"秋"的概率.(请用画树状图的方法说明理由)
(1)若从盒子中任意抽取1张书签,恰好抽到"夏"的概率为
$\frac{1}{4}$
;(2)若从盒子中任意抽取2张书签,求抽取的书签恰好1张为"春"、1张为"秋"的概率.(请用画树状图的方法说明理由)
答案:
$ \frac{1}{4}$
解:画树状图如下:
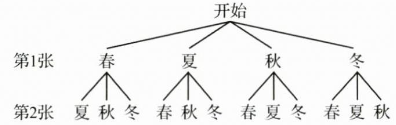
\ 共有12种等可能的结果,其中抽取的书签恰好1张为“春”,
1张为“秋”的结果有2种,
所以抽取的书签恰好1张为“春”,1张为“秋”的概率为$\frac{2}{12}=\frac{1}{6}$
$ \frac{1}{4}$
解:画树状图如下:

\ 共有12种等可能的结果,其中抽取的书签恰好1张为“春”,
1张为“秋”的结果有2种,
所以抽取的书签恰好1张为“春”,1张为“秋”的概率为$\frac{2}{12}=\frac{1}{6}$
15. 某款净水器使用寿命为十年,它的过滤功能主要由滤芯来实现.在使用过程中,需要不定期更换滤芯,每个滤芯200元.若在购买净水器的同时一次性购买多个滤芯,则滤芯可享受5折优惠;若在购买净水器之后再购买滤芯,则没有优惠;若购买的滤芯未使用,则按每个50元回收.如图是根据100位客户所购买的该款净水器在十年内更换滤芯的个数绘制的频数分布直方图.
(1)以这100位客户所购买的净水器在十年内更换滤芯的个数为样本,估计一台净水器在十年内更换滤芯的个数不大于10的概率;
(2)试以这100位客户所购买的净水器在十年内购买滤芯所需总费用的平均数作为决策依据,说明购买净水器的同时一次性购买11个还是12个滤芯.

(1)以这100位客户所购买的净水器在十年内更换滤芯的个数为样本,估计一台净水器在十年内更换滤芯的个数不大于10的概率;
(2)试以这100位客户所购买的净水器在十年内购买滤芯所需总费用的平均数作为决策依据,说明购买净水器的同时一次性购买11个还是12个滤芯.

答案:解:(1)P(一台净水器在十年内更换滤芯的个数
不大于$10)=\frac{10+20}{100}=\frac{3}{10}$
(2)若同时一次性购买11个滤芯,则所需总费用的平均数为
$\frac{1}{10}×(100×11-2×50)+\frac{1}{5}×(100×11-1×50)+$
$\frac{2}{5}×100×11+\frac{3}{10}×(100×11+200)=1140($元)
若同时一次性购买11个滤芯,则所需总费用的平均数为
$\frac{1}{10}×(100×12-3×50)+\frac{1}{5}×(100×12-2×50)+$
$\frac{2}{5}×(100×12-1×50)+\frac{3}{10}×100×12=1145($元)
∴购买净水器的同时一次性购买11个滤芯
不大于$10)=\frac{10+20}{100}=\frac{3}{10}$
(2)若同时一次性购买11个滤芯,则所需总费用的平均数为
$\frac{1}{10}×(100×11-2×50)+\frac{1}{5}×(100×11-1×50)+$
$\frac{2}{5}×100×11+\frac{3}{10}×(100×11+200)=1140($元)
若同时一次性购买11个滤芯,则所需总费用的平均数为
$\frac{1}{10}×(100×12-3×50)+\frac{1}{5}×(100×12-2×50)+$
$\frac{2}{5}×(100×12-1×50)+\frac{3}{10}×100×12=1145($元)
∴购买净水器的同时一次性购买11个滤芯