三、解答题(本大题共有 10 题,共 96 分。解答需写出必要的文字说明、演算步骤或证明过程)
19. 解答下列各题(每小题 4 分,共 12 分)
(1)计算:$\sqrt{12} - 4\tan 60^{\circ} + (-2 + \sqrt{3})^{-1}$。
(2)先化简,再求值:$\frac{x^{2} - 4x + 4}{2x - 4}·(x + 2)$,其中 $x = \sqrt{5}$。
(3)解不等式组:$\begin{cases}5x - 2 > 3(x - 2), \\1 - x \geq x - 5.\end{cases}$
19. 解答下列各题(每小题 4 分,共 12 分)
(1)计算:$\sqrt{12} - 4\tan 60^{\circ} + (-2 + \sqrt{3})^{-1}$。
(2)先化简,再求值:$\frac{x^{2} - 4x + 4}{2x - 4}·(x + 2)$,其中 $x = \sqrt{5}$。
(3)解不等式组:$\begin{cases}5x - 2 > 3(x - 2), \\1 - x \geq x - 5.\end{cases}$
答案:$19.(1)-2-3\sqrt{3}.(2)$化简,得$\frac{x^2-4}{2},$代入,得$\frac{1}{2}.(3)-2<x\leq3.$
解析:
(1) $\sqrt{12} - 4\tan 60^{\circ} + (-2 + \sqrt{3})^{-1}$
$=2\sqrt{3}-4×\sqrt{3}+\frac{1}{-2+\sqrt{3}}$
$=2\sqrt{3}-4\sqrt{3}+\frac{-2-\sqrt{3}}{(-2+\sqrt{3})(-2-\sqrt{3})}$
$=-2\sqrt{3}+\frac{-2-\sqrt{3}}{4 - 3}$
$=-2\sqrt{3}-2-\sqrt{3}$
$=-2 - 3\sqrt{3}$
(2) $\frac{x^{2} - 4x + 4}{2x - 4}·(x + 2)$
$=\frac{(x - 2)^2}{2(x - 2)}·(x + 2)$
$=\frac{x - 2}{2}·(x + 2)$
$=\frac{(x - 2)(x + 2)}{2}$
$=\frac{x^2 - 4}{2}$
当$x = \sqrt{5}$时,原式$=\frac{(\sqrt{5})^2 - 4}{2}=\frac{5 - 4}{2}=\frac{1}{2}$
(3) $\begin{cases}5x - 2 > 3(x - 2)① \\1 - x \geq x - 5②\end{cases}$
解①得:$5x - 2>3x - 6$
$5x - 3x>-6 + 2$
$2x>-4$
$x>-2$
解②得:$1 + 5\geq x + x$
$6\geq 2x$
$x\leq 3$
所以不等式组的解集为$-2<x\leq3$
$=2\sqrt{3}-4×\sqrt{3}+\frac{1}{-2+\sqrt{3}}$
$=2\sqrt{3}-4\sqrt{3}+\frac{-2-\sqrt{3}}{(-2+\sqrt{3})(-2-\sqrt{3})}$
$=-2\sqrt{3}+\frac{-2-\sqrt{3}}{4 - 3}$
$=-2\sqrt{3}-2-\sqrt{3}$
$=-2 - 3\sqrt{3}$
(2) $\frac{x^{2} - 4x + 4}{2x - 4}·(x + 2)$
$=\frac{(x - 2)^2}{2(x - 2)}·(x + 2)$
$=\frac{x - 2}{2}·(x + 2)$
$=\frac{(x - 2)(x + 2)}{2}$
$=\frac{x^2 - 4}{2}$
当$x = \sqrt{5}$时,原式$=\frac{(\sqrt{5})^2 - 4}{2}=\frac{5 - 4}{2}=\frac{1}{2}$
(3) $\begin{cases}5x - 2 > 3(x - 2)① \\1 - x \geq x - 5②\end{cases}$
解①得:$5x - 2>3x - 6$
$5x - 3x>-6 + 2$
$2x>-4$
$x>-2$
解②得:$1 + 5\geq x + x$
$6\geq 2x$
$x\leq 3$
所以不等式组的解集为$-2<x\leq3$
20. (8 分)如图,在矩形 $ABCD$ 中,点 $E$、$F$ 分别在边 $BA$、$DC$ 的延长线上,且$AE = \frac{1}{2}AB$,$CF = \frac{1}{2}CD$,连接 $EF$,分别交 $AD$、$BC$ 于点 $G$、$H$。求证:$DG = BH$。
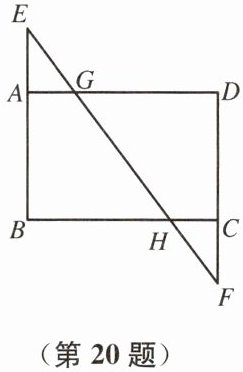

答案:证明:因为四边形ABCD是矩形
所以AB//CD且AB=CD,∠B=∠D=90°
所以∠E=∠F
因为$AE=\frac {1}{2}AB,$$CF=\frac {1}{2}CD,$AB=CD
所以AE=CF
所以BE= DF
在△BEH和△DFG 中
$\begin{cases}{∠E=∠F }\\{BE=DF}\\{∠B=∠D} \end{cases}$
所以$△BEH≌△DFG(\mathrm {ASA})$
所以DG=BH
所以AB//CD且AB=CD,∠B=∠D=90°
所以∠E=∠F
因为$AE=\frac {1}{2}AB,$$CF=\frac {1}{2}CD,$AB=CD
所以AE=CF
所以BE= DF
在△BEH和△DFG 中
$\begin{cases}{∠E=∠F }\\{BE=DF}\\{∠B=∠D} \end{cases}$
所以$△BEH≌△DFG(\mathrm {ASA})$
所以DG=BH