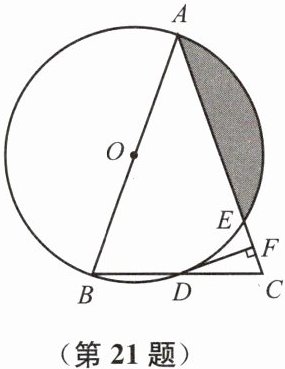
21. (10 分)如图,在$\triangle ABC$中,$AB = AC$,以 $AB$ 为直径的$\odot O$分别与 $BC$、$AC$交于点 $D$、$E$,过点 $D$ 作 $DF ⊥ AC$,垂足为 $F$,已知$\odot O$的半径为 $4\sqrt{3}$,$\angle CDF = 15^{\circ}$。
(1)求$\angle BAC$的度数;
(2)求阴影部分的面积。
(1)求$\angle BAC$的度数;
(2)求阴影部分的面积。

答案:解:(1)因为DF⊥AC,∠CDF=15°
所以∠C=75°
因为AB=AC
所以∠ABC=∠C=75°
所以∠BAC=180°-75°×2=30°
(2)因为圆O的半径为$4\sqrt{3}$
所以$AO=OE=4\sqrt{3}$
因为∠BAC=30°,
所以∠AEO=30°,∠AOE=120°
所以$S_{△AOE}=\frac {1}{2}×4\sqrt{3}×4\sqrt{3}×\frac {\sqrt{3}}{2}=12\sqrt{3}$
$S_{扇形}=\frac {120°}{360°}×π×(4\sqrt{3})²=16π$
所以$S_{阴影部分}=16π-12\sqrt{3}$
所以∠C=75°
因为AB=AC
所以∠ABC=∠C=75°
所以∠BAC=180°-75°×2=30°
(2)因为圆O的半径为$4\sqrt{3}$
所以$AO=OE=4\sqrt{3}$
因为∠BAC=30°,
所以∠AEO=30°,∠AOE=120°
所以$S_{△AOE}=\frac {1}{2}×4\sqrt{3}×4\sqrt{3}×\frac {\sqrt{3}}{2}=12\sqrt{3}$
$S_{扇形}=\frac {120°}{360°}×π×(4\sqrt{3})²=16π$
所以$S_{阴影部分}=16π-12\sqrt{3}$
22. (8 分)小莉爸爸买了一张音乐会的门票,她和哥哥两人都很想去观看,可门票只有一张,九年级的哥哥想了一个办法,拿了 8 张扑克牌,将数字为 1、2、3、5 的 4 张牌给小莉,将数字为 4、6、7、8 的 4 张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的 4 张牌中随机抽出一张,然后将抽出的两张扑克牌的数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去。
请用画树状图或列表的方法判断哥哥设计的规则是否公平。
请用画树状图或列表的方法判断哥哥设计的规则是否公平。
答案:
解:列表如下:
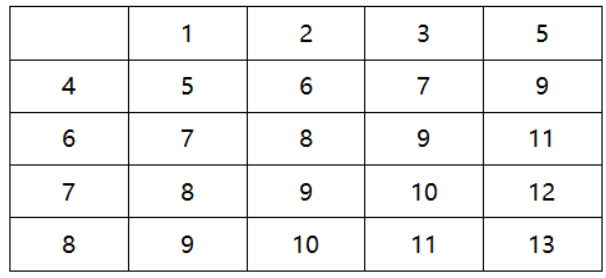
共有16种等可能的结果,
其中小莉去的结果有6种,哥哥去的结果有10种,
所以P(小莉去$)=\frac {6}{16}=\frac {3}{8}$
P(哥哥去$) = \frac {10}{16}=\frac {5}{8}$
P(小莉去$) \lt P($哥哥去) ,
故哥哥设计的规则不公平。
解:列表如下:

共有16种等可能的结果,
其中小莉去的结果有6种,哥哥去的结果有10种,
所以P(小莉去$)=\frac {6}{16}=\frac {3}{8}$
P(哥哥去$) = \frac {10}{16}=\frac {5}{8}$
P(小莉去$) \lt P($哥哥去) ,
故哥哥设计的规则不公平。