24. (10 分)一公司面向社会招聘机械制造类和规划设计类工作人员共 150 名,其中机械制造类人员工资为 6000 元/月,规划设计类人员工资为 10000 元/月。
(1)若要求本次招聘的规划设计人员不少于机械制造人员的 2 倍,且要使公司每月所付工资总额最少,则这两类人员各招多少名?此时最少工资总额是多少?
(2)在(1)的条件下,因这两类人员表现出色,公司决定另用 50 万元奖励他们,其中机械制造人员人均奖金不得超过规划设计人员的人均奖金,但不低于 1000 元,试求规划设计类人员的人均奖金的取值范围。
(1)若要求本次招聘的规划设计人员不少于机械制造人员的 2 倍,且要使公司每月所付工资总额最少,则这两类人员各招多少名?此时最少工资总额是多少?
(2)在(1)的条件下,因这两类人员表现出色,公司决定另用 50 万元奖励他们,其中机械制造人员人均奖金不得超过规划设计人员的人均奖金,但不低于 1000 元,试求规划设计类人员的人均奖金的取值范围。
答案:解: (1)设机械制造人员招x名,则规划设计人员招(150-x)名,
此时工资总额为y元。
由题意得,
y= 6000x + 10000(150 - x)
= 1500000 - 4000x
因为$-4000\lt 0 . $
所以y随x的增大而减小
因为规划设计人员不少于机械制造人员的2倍
所以150-x≤2x
解得,x≥50
所以当x = 50时, y取最小值,最小值为1500000-4000×50= 1300000
答:械制造人员招50名,规划设计人员招100名,此时最少工资总额
为1300000元。
(2)设规划设计类人员的人均奖金为k元。
由题意得,$1000 ≤\frac {500000-100k}{50}≤k,$
解得$\frac {10000}{3}≤k≤4500$
答:规划设计类,人员的人均奖金的取值范围为$\frac {10000}{3}\sim 4500yuan .$
此时工资总额为y元。
由题意得,
y= 6000x + 10000(150 - x)
= 1500000 - 4000x
因为$-4000\lt 0 . $
所以y随x的增大而减小
因为规划设计人员不少于机械制造人员的2倍
所以150-x≤2x
解得,x≥50
所以当x = 50时, y取最小值,最小值为1500000-4000×50= 1300000
答:械制造人员招50名,规划设计人员招100名,此时最少工资总额
为1300000元。
(2)设规划设计类人员的人均奖金为k元。
由题意得,$1000 ≤\frac {500000-100k}{50}≤k,$
解得$\frac {10000}{3}≤k≤4500$
答:规划设计类,人员的人均奖金的取值范围为$\frac {10000}{3}\sim 4500yuan .$
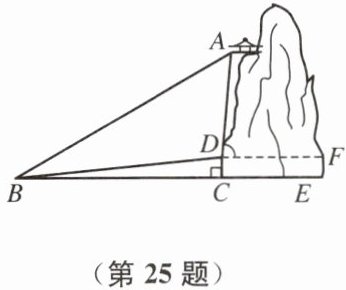
25. (10 分)某景区有一个景观奇异的天门洞,点 $D$ 是洞的人口,游人从人口进洞游览后,可经山洞到达山顶的凉亭 $A$ 处观看旅游区风景,最后坐缆车沿索道 $AB$返回山脚下的 $B$ 处。在同一平面内,若测得斜坡 $BD$ 的长为 $1000m$,坡角$\angle DBC = 5^{\circ}$,在 $B$ 处测得凉亭 $A$ 的仰角$\angle ABC = 35^{\circ}$,在 $D$ 处测得凉亭 $A$ 的仰角$\angle ADF = 80^{\circ}$,过点 $D$ 作地面 $BE$ 的垂线,垂足为 $C$。
(1)求$\angle ADB$的度数;
(2)求索道 $AB$ 的长(保留根号)。
(1)求$\angle ADB$的度数;
(2)求索道 $AB$ 的长(保留根号)。

答案:
解: (1)由题意得,∠DBC=5°,∠ADF=80°,
∠DCB=90° ,∠CDF=90°
因为∠DBC=5°,∠DCB=90°
所以∠BDC=85°
因为∠CDF=90°,∠ADF=80°
所以∠ADB= 360°-85°-90°-80°=105°
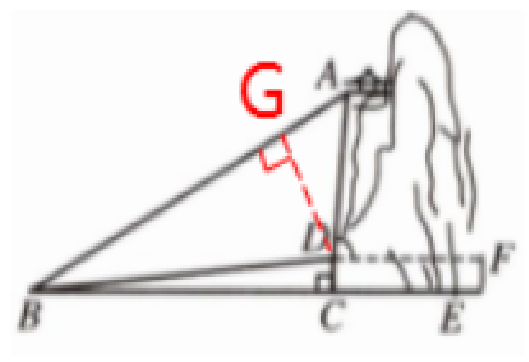
(2)过点D作DG⊥AB ,垂足为点G ,如图所示
因为∠ABC=35°,∠DBC=5°
所以∠DBG= 30°
因为∠ADB=105°
所以∠DAG=45°
在Rt△DBG 中
因为∠DBG=30° , BD=1000m
所以DG = BD×sin{30}° = 500m,$BG = BD×cos{30}°= 500\sqrt{3}m$
在Rt△DAG 中
因为DG= 500m ,∠DAG=45°
所以AG= DG= 500m
所以$AB=BG+AG=(500+500\sqrt{3})m$
解: (1)由题意得,∠DBC=5°,∠ADF=80°,
∠DCB=90° ,∠CDF=90°
因为∠DBC=5°,∠DCB=90°
所以∠BDC=85°
因为∠CDF=90°,∠ADF=80°
所以∠ADB= 360°-85°-90°-80°=105°
(2)过点D作DG⊥AB ,垂足为点G ,如图所示

因为∠ABC=35°,∠DBC=5°
所以∠DBG= 30°
因为∠ADB=105°
所以∠DAG=45°
在Rt△DBG 中
因为∠DBG=30° , BD=1000m
所以DG = BD×sin{30}° = 500m,$BG = BD×cos{30}°= 500\sqrt{3}m$
在Rt△DAG 中
因为DG= 500m ,∠DAG=45°
所以AG= DG= 500m
所以$AB=BG+AG=(500+500\sqrt{3})m$