26. (10 分)勾股定理是数学史上非常重要的一个定理。早在 2000 多年以前,人们就开始对它进行研究,至今已有几百种证明方法。在欧几里得编纂的《原本》中证明勾股定理的方法如下,请仔细阅读并解答问题。
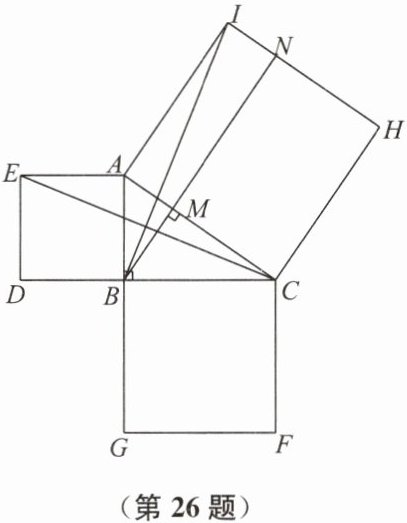
如图,分别以 $Rt\triangle ABC$ 的三边为边长,向外作正方形 $ABDE$、$BCFG$、$ACHI$。
(1)连接 $BI$、$CE$,求证:$\triangle ABI \cong \triangle AEC$。
(2)过点 $B$ 作 $AC$ 的垂线,交 $AC$ 于点 $M$,交 $IH$ 于点 $N$。
① 试说明四边形 $AMNI$ 与正方形 $ABDE$ 的面积相等;
② 请直接写出图中与正方形 $BCFG$ 面积相等的四边形。
(3)由第(2)题可得:正方形 $ABDE$ 的面积+正方形 $BCFG$ 的面积=
如图,分别以 $Rt\triangle ABC$ 的三边为边长,向外作正方形 $ABDE$、$BCFG$、$ACHI$。
(1)连接 $BI$、$CE$,求证:$\triangle ABI \cong \triangle AEC$。
(2)过点 $B$ 作 $AC$ 的垂线,交 $AC$ 于点 $M$,交 $IH$ 于点 $N$。
① 试说明四边形 $AMNI$ 与正方形 $ABDE$ 的面积相等;
② 请直接写出图中与正方形 $BCFG$ 面积相等的四边形。
(3)由第(2)题可得:正方形 $ABDE$ 的面积+正方形 $BCFG$ 的面积=
正方形AIHC
的面积,即在 $Rt\triangle ABC$ 中,$AB^{2} + BC^{2} =$$AC^{2}$
。
答案:证明:(1)因为四边形ABDE、ACHI为正方形
所以AB=AE , AI=AC,∠CAI=∠EAB=90°
所以∠BAI=∠EAC
在△ABI 和△AEC中,
$\begin{cases}{AB=AE }\\{∠BAI=∠EAC}\\{AI=AC} \end{cases}$
所以$△ABI≌△AEC(\mathrm {SAS})$
(2)①因为$S_{四边形}AMNI= AI ×AM,$
$S_{△ABI}=\frac {1}{2}×AI×AM$
所以$S_{四边形}AMNI = 2S_{△ABI} ,$
同理, S 正方形$BCFG= 2S_{△AEC}$
因为△ABI≌△AEC,
所以$S_{△ABI}= S_{△AEC}$
所以$S_{四边形}AMNI = S $正方形BCFG
②四边形MCHN
AC²
正方形ACHI
所以AB=AE , AI=AC,∠CAI=∠EAB=90°
所以∠BAI=∠EAC
在△ABI 和△AEC中,
$\begin{cases}{AB=AE }\\{∠BAI=∠EAC}\\{AI=AC} \end{cases}$
所以$△ABI≌△AEC(\mathrm {SAS})$
(2)①因为$S_{四边形}AMNI= AI ×AM,$
$S_{△ABI}=\frac {1}{2}×AI×AM$
所以$S_{四边形}AMNI = 2S_{△ABI} ,$
同理, S 正方形$BCFG= 2S_{△AEC}$
因为△ABI≌△AEC,
所以$S_{△ABI}= S_{△AEC}$
所以$S_{四边形}AMNI = S $正方形BCFG
②四边形MCHN
AC²
正方形ACHI
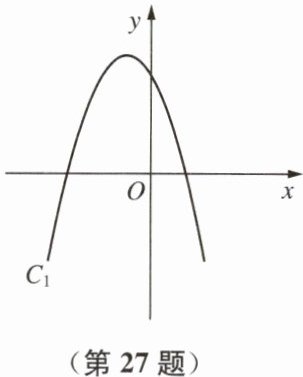
27. (10 分)已知抛物线 $C_{1}$ 与 $x$ 轴的一个交点为$(-4,0)$,对称轴所在直线相应的函数表达式为 $x = -1.5$,且该抛物线过点$(-1,6)$。
(1)求抛物线 $C_{1}$ 相应的函数表达式。
(2)求出与抛物线 $C_{1}$ 关于原点对称的抛物线 $C_{2}$ 相应的函数表达式,并在 $C_{1}$ 所在的平面直角坐标系中画出 $C_{2}$ 的图像。
(3)在(2)的条件下,抛物线 $C_{1}$ 与抛物线 $C_{2}$ 相交于 $A$、$B$ 两点(点 $A$ 在点 $B$ 的左侧)。若点 $P$ 在抛物线 $C_{1}$ 上,且位于点 $A$ 和点 $B$ 之间;点 $Q$ 在抛物线 $C_{2}$ 上,也位于点 $A$ 和点 $B$ 之间。当 $PQ // y$ 轴时,求 $PQ$ 的最大值。
(1)求抛物线 $C_{1}$ 相应的函数表达式。
(2)求出与抛物线 $C_{1}$ 关于原点对称的抛物线 $C_{2}$ 相应的函数表达式,并在 $C_{1}$ 所在的平面直角坐标系中画出 $C_{2}$ 的图像。
(3)在(2)的条件下,抛物线 $C_{1}$ 与抛物线 $C_{2}$ 相交于 $A$、$B$ 两点(点 $A$ 在点 $B$ 的左侧)。若点 $P$ 在抛物线 $C_{1}$ 上,且位于点 $A$ 和点 $B$ 之间;点 $Q$ 在抛物线 $C_{2}$ 上,也位于点 $A$ 和点 $B$ 之间。当 $PQ // y$ 轴时,求 $PQ$ 的最大值。

答案:
解: (1)设抛物线${C}_1$的函数表达式为y= ax²+ bx +c
由题意得,
$\begin{cases}{0=16a-4b+c}\\{-\dfrac {b}{2a}=-1.5}\\{6=a-b+c} \end{cases}$
解得a=-1,b=-3,c=4
所以抛物线${C}_1$的函数表达式为y= -x²- 3x +4
(2)抛物线${C}_2$的图像如图所示,
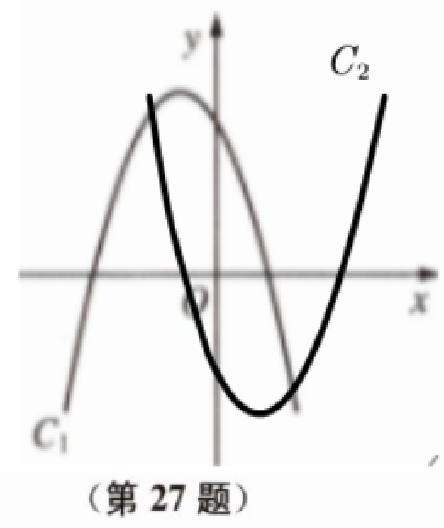
设抛物线${C}_2$的函数表达式为y= dx²+ex+f ,
则抛物线${C}_2$与x轴交点为(4 , 0) ,对称轴所在直线为x = 1.5,
且抛物线过点(1.-6)。
由题意得,
$\begin{cases}{16d+4e+f=0 }\\{-\dfrac {c}{2d}=1.5}\\{d+e+f=-6} \end{cases}$
所以d=1,e=-3,f=-4
抛物线${C}_2$的函数表达式为y=x²-3x-4
(3)由题意得,-x²-3x+4=x²-3x-4,
解得,x=±2
所以点A横坐标为-2 ,点B横坐标为2
设点P的横坐标为t ,则点P坐标为(t,-t² - 3t +4)
因为PQ//y轴,点P的横坐标为t ,
所以点Q的横坐标也为t
因为点Q在抛物线${C}_2$上,
所以点$Q_{坐标} $为(t,t²- 3t- 4)
所以PQ=(-t²-3t+4)- (t²- 3t-4)=-2t²+ 8
因为点P位于点A和点B之间,
解: (1)设抛物线${C}_1$的函数表达式为y= ax²+ bx +c
由题意得,
$\begin{cases}{0=16a-4b+c}\\{-\dfrac {b}{2a}=-1.5}\\{6=a-b+c} \end{cases}$
解得a=-1,b=-3,c=4
所以抛物线${C}_1$的函数表达式为y= -x²- 3x +4
(2)抛物线${C}_2$的图像如图所示,

设抛物线${C}_2$的函数表达式为y= dx²+ex+f ,
则抛物线${C}_2$与x轴交点为(4 , 0) ,对称轴所在直线为x = 1.5,
且抛物线过点(1.-6)。
由题意得,
$\begin{cases}{16d+4e+f=0 }\\{-\dfrac {c}{2d}=1.5}\\{d+e+f=-6} \end{cases}$
所以d=1,e=-3,f=-4
抛物线${C}_2$的函数表达式为y=x²-3x-4
(3)由题意得,-x²-3x+4=x²-3x-4,
解得,x=±2
所以点A横坐标为-2 ,点B横坐标为2
设点P的横坐标为t ,则点P坐标为(t,-t² - 3t +4)
因为PQ//y轴,点P的横坐标为t ,
所以点Q的横坐标也为t
因为点Q在抛物线${C}_2$上,
所以点$Q_{坐标} $为(t,t²- 3t- 4)
所以PQ=(-t²-3t+4)- (t²- 3t-4)=-2t²+ 8
因为点P位于点A和点B之间,