28. (10 分)若一个点能与另外两个点构成直角三角形,则称这个点为另外两个点的勾股点。例如,在矩形 $ABCD$ 中,点 $C$ 与点 $A$、$B$ 构成 $Rt\triangle ABC$,则称点 $C$ 为 $A$、$B$ 两点的勾股点。同样,点 $D$ 也是 $A$、$B$ 两点的勾股点。
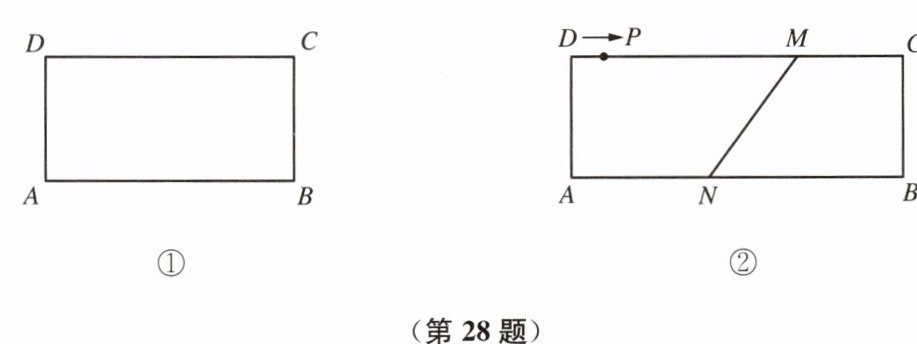
(1)如图①,在矩形 $ABCD$ 中,$AB = 2$,$BC = 1$,请在边 $CD$ 上作出 $A$、$B$ 两点的勾股点(点 $C$ 和点 $D$ 除外)。(要求:用直尺和圆规作图,保留作图痕迹,不要求写作法)
(2)如图②,在矩形 $ABCD$ 中,$AB = 12cm$,$BC = 4cm$,$DM = 8cm$,$AN = 5cm$。动点 $P$ 从点 $D$ 出发沿着 $DC$ 方向以 $1cm/s$ 的速度向右移动,过点 $P$ 的直线 $l$ 平行于 $BC$,当动点 $P$ 运动到点 $M$ 时停止运动。设运动时间为 $t(s)$,点 $H$ 为 $M$、$N$ 两点的勾股点,且点 $H$ 在直线 $l$ 上。
① 当 $t = 4$ 时,求 $PH$ 的长;
② 探究满足条件的点 $H$ 的个数(直接写出点 $H$ 的个数及相应 $t$ 的取值范围,不必证明)。
(1)如图①,在矩形 $ABCD$ 中,$AB = 2$,$BC = 1$,请在边 $CD$ 上作出 $A$、$B$ 两点的勾股点(点 $C$ 和点 $D$ 除外)。(要求:用直尺和圆规作图,保留作图痕迹,不要求写作法)
(2)如图②,在矩形 $ABCD$ 中,$AB = 12cm$,$BC = 4cm$,$DM = 8cm$,$AN = 5cm$。动点 $P$ 从点 $D$ 出发沿着 $DC$ 方向以 $1cm/s$ 的速度向右移动,过点 $P$ 的直线 $l$ 平行于 $BC$,当动点 $P$ 运动到点 $M$ 时停止运动。设运动时间为 $t(s)$,点 $H$ 为 $M$、$N$ 两点的勾股点,且点 $H$ 在直线 $l$ 上。
① 当 $t = 4$ 时,求 $PH$ 的长;
② 探究满足条件的点 $H$ 的个数(直接写出点 $H$ 的个数及相应 $t$ 的取值范围,不必证明)。

答案:
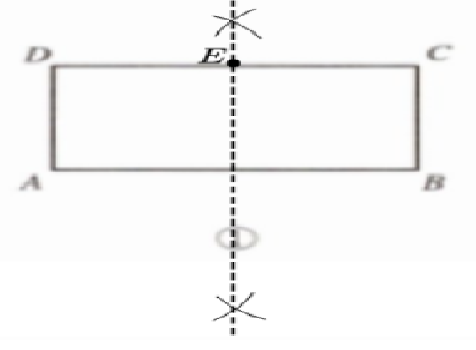
解:(1)如图所示:点E即为所求.
(2)4个.理由如下:
连接AP,BP.
∵△ABP为直角三角形,
∴∠APB=90°,
∴∠DPA+∠CPB=90°.
∵∠DAP+APD=90°,
∴∠DAP=CPB.
又
∵∠D=∠C,
∴△DPA∽△BCP,
∴$\frac {DP}{AD}=\frac {CB}{PC}.$
设DP=x,则PC=3-x,则$\frac {x}{1}=\frac {1}{3-x},$
解得:$x=\frac {3±\sqrt{5}}{2},$
∴$DP=\frac {3±\sqrt{5}}{2}.$
∵D,C也是A,B的勾股点,点P的位置有两个,
∴共有4个勾股点.
(3)①如图所示:当t=4时,DP=4,AE=4,PE=AD=4,
∵DM=8,AN=5,
∴PM=4,EN=1.
过点N作NG⊥PM于点G,则PG=EN=1,
则$tan∠PMN=\frac {NG}{GM}=\frac {4}{4-1}=\frac {4}{3}.$
当$∠NMH_1=90°$时,则$∠PH_1M+∠H_1MP=∠H_1MP+∠NMP=90°,$
∴$∠PH_1M=∠NMP,$
∴$tan∠PH_1M=\frac {PM}{P{H_1}_1}=tan∠NMP=\frac {4}{3},$
∴$PH_1=\frac {3}{4}×4=3;$
当$∠MNH_3=90°$时,可得$H_1M//H_3N,$
∴$∠NH_3E=∠MH_1P,$
∴$tan∠NH_3E=tan∠PH_1M=\frac {4}{3},$
∴$\frac {EN}{{H}_3E}=\frac {1}{{H}_3E}=\frac {4}{3},$
∴$H_3E=\frac {3}{4},$
∴$PH_3=4-\frac {3}{4}=\frac {13}{4}.$
当$∠PH_2N=90°$时,设$PH_2=x,$则$H_2E=4-x,$
∵$∠PMH_2+∠PH_2M=90°,$$∠PH_2M+∠EH_2N=90°,$
∴$∠PMH_2=∠NH_2E.$
∵∠MPE=∠PEN=90°,
∴$△PMH_2∽△EH_2N,$
∴$\frac {P{H}_2}{EN}=\frac {PM}{E{H}_2},$
即:$\frac {x}{1}=\frac {4}{4-x},$
解得:x=2,经检验适合题意,
∴$PH_2=2.$
综上:PH为2或3或$\frac {13}{4}.$
②由①可知,当t=4时,MN=5,$PH_2=2,$
∴$H_2$是PE的中点,
设以MN为直径的圆O,则$OH_2$是梯形PMNE的中位线,
∴$OH_2=\frac {1}{2}(PM+EN)=\frac {1}{2}×(1+4)=2.5=\frac {1}{2}MN,$且$OH_2⊥PE,$
∴圆O与PE相切,
∴PE与圆O只有一个交点,
结合当M,N为直角顶点时,得到两个直角三角形,
∴此时共有3个勾股点.
当0≤t<4时,PE与圆O相离,PE与圆O没有交点,
此时,只有当M,N为直角顶点时,得到两个直角三角形,
∴此时有两个勾股点.
当t=5或t=8时,PE通过N或M点,此时有两个勾股点,
当4≤t<5或5<t<8时,直线PE与圆O有两个交点,
结合当M,N为直角顶点时,得到两个直角三角形,
共有4个勾股点.
综上:当0≤t<4时或t=5或t=8时,有2个勾股点,
当t=4时,有3个勾股点,
当4<t<5时或5<t<8时,有4个勾股点,
当4<t<5时,有4个勾股点,当t=5时,有2个勾股点.
解:(1)如图所示:点E即为所求.

(2)4个.理由如下:
连接AP,BP.
∵△ABP为直角三角形,
∴∠APB=90°,
∴∠DPA+∠CPB=90°.
∵∠DAP+APD=90°,
∴∠DAP=CPB.
又
∵∠D=∠C,
∴△DPA∽△BCP,
∴$\frac {DP}{AD}=\frac {CB}{PC}.$
设DP=x,则PC=3-x,则$\frac {x}{1}=\frac {1}{3-x},$
解得:$x=\frac {3±\sqrt{5}}{2},$
∴$DP=\frac {3±\sqrt{5}}{2}.$
∵D,C也是A,B的勾股点,点P的位置有两个,
∴共有4个勾股点.
(3)①如图所示:当t=4时,DP=4,AE=4,PE=AD=4,
∵DM=8,AN=5,
∴PM=4,EN=1.
过点N作NG⊥PM于点G,则PG=EN=1,
则$tan∠PMN=\frac {NG}{GM}=\frac {4}{4-1}=\frac {4}{3}.$
当$∠NMH_1=90°$时,则$∠PH_1M+∠H_1MP=∠H_1MP+∠NMP=90°,$
∴$∠PH_1M=∠NMP,$
∴$tan∠PH_1M=\frac {PM}{P{H_1}_1}=tan∠NMP=\frac {4}{3},$
∴$PH_1=\frac {3}{4}×4=3;$
当$∠MNH_3=90°$时,可得$H_1M//H_3N,$
∴$∠NH_3E=∠MH_1P,$
∴$tan∠NH_3E=tan∠PH_1M=\frac {4}{3},$
∴$\frac {EN}{{H}_3E}=\frac {1}{{H}_3E}=\frac {4}{3},$
∴$H_3E=\frac {3}{4},$
∴$PH_3=4-\frac {3}{4}=\frac {13}{4}.$
当$∠PH_2N=90°$时,设$PH_2=x,$则$H_2E=4-x,$
∵$∠PMH_2+∠PH_2M=90°,$$∠PH_2M+∠EH_2N=90°,$
∴$∠PMH_2=∠NH_2E.$
∵∠MPE=∠PEN=90°,
∴$△PMH_2∽△EH_2N,$
∴$\frac {P{H}_2}{EN}=\frac {PM}{E{H}_2},$
即:$\frac {x}{1}=\frac {4}{4-x},$
解得:x=2,经检验适合题意,
∴$PH_2=2.$
综上:PH为2或3或$\frac {13}{4}.$
②由①可知,当t=4时,MN=5,$PH_2=2,$
∴$H_2$是PE的中点,
设以MN为直径的圆O,则$OH_2$是梯形PMNE的中位线,
∴$OH_2=\frac {1}{2}(PM+EN)=\frac {1}{2}×(1+4)=2.5=\frac {1}{2}MN,$且$OH_2⊥PE,$
∴圆O与PE相切,
∴PE与圆O只有一个交点,
结合当M,N为直角顶点时,得到两个直角三角形,
∴此时共有3个勾股点.
当0≤t<4时,PE与圆O相离,PE与圆O没有交点,
此时,只有当M,N为直角顶点时,得到两个直角三角形,
∴此时有两个勾股点.
当t=5或t=8时,PE通过N或M点,此时有两个勾股点,
当4≤t<5或5<t<8时,直线PE与圆O有两个交点,
结合当M,N为直角顶点时,得到两个直角三角形,
共有4个勾股点.
综上:当0≤t<4时或t=5或t=8时,有2个勾股点,
当t=4时,有3个勾股点,
当4<t<5时或5<t<8时,有4个勾股点,
当4<t<5时,有4个勾股点,当t=5时,有2个勾股点.