3. 某商场出售某种工艺品. 若每个获利 $ x $ 元,一天可售出 $ (8 - x) $ 个,则当 $ x =$
4
时,一天出售该种工艺品的总利润 $ y $ 最大.答案:4
4. 某民俗旅游村为满足旅客住宿需要,开设了有 100 张床位的旅馆. 据调查,当每张床位每天收费 100 元时,床位可全部租出. 若每张床位每天收费提高 20 元,则租出的床位将减少 10 张. 如果以 20 元为单位调整每张床位每天的收费,为使租出的床位少且总租金高,那么每张床位每天最合适的收费是
160
元.答案:160
三、解答题
5. 某商店将进价为 80 元/件的某种商品按 100 元/件出售,一天可销出 100 件. 该店想通过降低售价、增加销售量的办法来提高利润. 经过市场调查,发现这种商品的单价每降低 1 元,销售量可增加 10 件. 这种商品的售价降低多少时,能使销售利润最大?最大利润为多少元?
5. 某商店将进价为 80 元/件的某种商品按 100 元/件出售,一天可销出 100 件. 该店想通过降低售价、增加销售量的办法来提高利润. 经过市场调查,发现这种商品的单价每降低 1 元,销售量可增加 10 件. 这种商品的售价降低多少时,能使销售利润最大?最大利润为多少元?
答案: 解:设这种商品的售价降低x元,此时的销售利润为y元。
由题意得,
y= (100- x - 80)(100 + 10x)
= (20-x)(100 + 10x)
= -10x²+ 100x + 2000
= -10(x-5)²+ 2250
因为$-10\lt 0$
所以抛物线开口向下,当x = 5时, y取最大值,最大值为2250
所以这种商品的售价降低5元时,能使销售利润最大,最大利润为2250元。
由题意得,
y= (100- x - 80)(100 + 10x)
= (20-x)(100 + 10x)
= -10x²+ 100x + 2000
= -10(x-5)²+ 2250
因为$-10\lt 0$
所以抛物线开口向下,当x = 5时, y取最大值,最大值为2250
所以这种商品的售价降低5元时,能使销售利润最大,最大利润为2250元。
6. 某产品每件成本 10 元,试销阶段每件产品的日销售价 $ x $(元)与产品的日销售量 $ y $(件)之间的关系如下表:

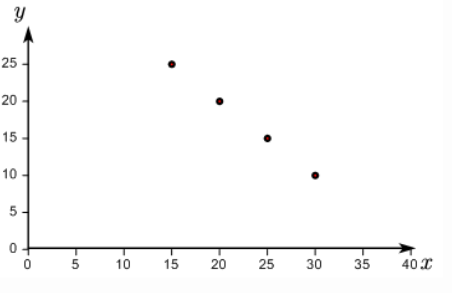
(1)根据表中数据在平面直角坐标系上描点,观察点的分布,建立关于 $ y $ 与 $ x $ 的合适的函数模型.
(2)根据(1)中所确定的函数模型,问:要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?

(1)根据表中数据在平面直角坐标系上描点,观察点的分布,建立关于 $ y $ 与 $ x $ 的合适的函数模型.
(2)根据(1)中所确定的函数模型,问:要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
答案:
解:(1)y=-x+ 40
(2)设每日销售利润为z元
z=(x- 10)(-x + 40)
= -x²+50x- 400
=-(x- 25)²+ 225
当x= 25时,z有最大值225
每件产品应定为25元,此时每日销售利润是225元
解:(1)y=-x+ 40

(2)设每日销售利润为z元
z=(x- 10)(-x + 40)
= -x²+50x- 400
=-(x- 25)²+ 225
当x= 25时,z有最大值225
每件产品应定为25元,此时每日销售利润是225元