1. 已知 $ C $ 是线段 $ AB $ 的黄金分割点 $ (AC>BC) $,则 $ AC $ 是线段
AB
与线段BC
的比例中项. 如果 $ AB = 100 \, \mathrm{cm} $,那么 $ AC \approx $61.8
$ \mathrm{cm} $,$ BC \approx $38.2
$ \mathrm{cm} $(精确到 $ 0.1 \, \mathrm{cm} $).答案:AB
BC
61.8
38.2
BC
61.8
38.2
2. 顶角为 $ 36^{\circ} $ 的等腰三角形的底与腰的比恰好等于黄金数,这种三角形称为“黄金三角形”. 如图,$ \triangle ABC $ 为黄金三角形,其中 $ \angle A = 36^{\circ} $. 若 $ BD $ 为 $ \angle ABC $ 的平分线,$ CE $ 是 $ \angle ACB $ 的平分线,$ BD $、$ CE $ 相交于点 $ O $,则图中的黄金三角形有

5
个.
答案:5
二、解答题
3. 如图,已知 $ C $ 是线段 $ AB $ 的黄金分割点,且 $ AC<BC $. 若 $ AB = 10 \, \mathrm{cm} $,求 $ AC $ 的长(精确到 $ 0.01 \, \mathrm{cm} $).

3. 如图,已知 $ C $ 是线段 $ AB $ 的黄金分割点,且 $ AC<BC $. 若 $ AB = 10 \, \mathrm{cm} $,求 $ AC $ 的长(精确到 $ 0.01 \, \mathrm{cm} $).

答案:解:因为C是线段AB的黄金分割点,且$AC\lt BC$
所以$BC=\frac {\sqrt{5}-1}{2}AB$
因为$AB= 10\ \mathrm {cm}$
所以$BC≈6.18\ \mathrm {cm}$
所以$AC≈3.82\ \mathrm {cm}$
所以$BC=\frac {\sqrt{5}-1}{2}AB$
因为$AB= 10\ \mathrm {cm}$
所以$BC≈6.18\ \mathrm {cm}$
所以$AC≈3.82\ \mathrm {cm}$
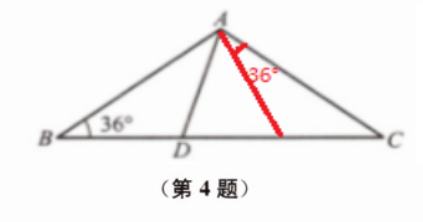
4. 如图,在底角为 $ 36^{\circ} $ 的等腰三角形 $ ABC $ 中,在 $ BC $ 上取黄金分割点 $ D (BD<CD) $,连接 $ AD $. 求 $ \triangle ABD $、$ \triangle ACD $ 各内角的度数. 你能仿照题中分割的方法再作出黄金三角形吗?


答案:
解: △ABC的各内角度数分别为36°、36°、 108°
△ACD各内角度数分别为36°、72°、72°
解: △ABC的各内角度数分别为36°、36°、 108°
△ACD各内角度数分别为36°、72°、72°

5. 宽与长之比为 $ \frac{\sqrt{5} - 1}{2} $ 的矩形称为黄金矩形. 试画出长为 $ 4 \, \mathrm{cm} $ 的黄金矩形.
答案:
解:黄金矩形的宽:$ 4×\frac {\sqrt{5}-1}{2}= 2\sqrt{5}- 2≈2.472(\ \mathrm {cm})$

解:黄金矩形的宽:$ 4×\frac {\sqrt{5}-1}{2}= 2\sqrt{5}- 2≈2.472(\ \mathrm {cm})$
