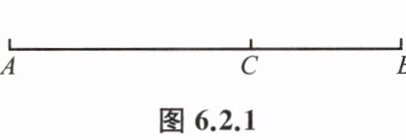
例 1 如图 6.2.1,已知 $ C $ 为线段 $ AB $ 的黄金分割点,且 $ AC>BC $.
求 $ \frac{AC}{AB} $ 的值.
求 $ \frac{AC}{AB} $ 的值.

答案:解:因为C为AB的黄金分割点,$AC \gt BC$
所以AC²= AB×BC= AB×(AB-AC)
所以$\frac {AC}{AB}=\frac {AB-AC}{AC}=\frac {AB}{AC}-1$
设$\frac {AC}{AB}=x$
则$x=\frac {1}{x}-1$
所以解得$x=\frac {\sqrt{5}-1}{2}$或$x=\frac {-\sqrt{5}-1}{2}($舍去)
所以$\frac {AC}{AB}=\frac {\sqrt{5}-1}{2}$
所以AC²= AB×BC= AB×(AB-AC)
所以$\frac {AC}{AB}=\frac {AB-AC}{AC}=\frac {AB}{AC}-1$
设$\frac {AC}{AB}=x$
则$x=\frac {1}{x}-1$
所以解得$x=\frac {\sqrt{5}-1}{2}$或$x=\frac {-\sqrt{5}-1}{2}($舍去)
所以$\frac {AC}{AB}=\frac {\sqrt{5}-1}{2}$
例 2 一般认为,人体肚脐以上部分(上半身)与肚脐以下部分(下半身)的高度比例越接近 $ 0.618 $,越给人以美感. 遗憾的是,即使是芭蕾舞演员也难以如此完美. 某女士身高 $ 1.68 \, \mathrm{m} $,肚脐以上部分为 $ 0.66 \, \mathrm{m} $,她应该选择穿多高的高跟鞋才能看起来更美呢(精确到 $ 0.1 \, \mathrm{cm} $)?
答案:解:$ 0.66m= 66\ \mathrm {cm}$
$1.68m= 168\ \mathrm {cm}$
$\frac {66}{0.618}-(168- 66)≈4.8(\ \mathrm {cm})$
答:她应选择穿$4.8\ \mathrm {cm}$的高跟鞋才能看起来更美。
$1.68m= 168\ \mathrm {cm}$
$\frac {66}{0.618}-(168- 66)≈4.8(\ \mathrm {cm})$
答:她应选择穿$4.8\ \mathrm {cm}$的高跟鞋才能看起来更美。