例 2 如图 6.3.2,△ABC∽△ADE.
(1)若∠BAC=75°,∠ABC=40°,求∠ADE 和∠AED 的度数;
(2)若 AB=30 cm,BD=18 cm,BC=20 cm,求 DE 的长.

(1)若∠BAC=75°,∠ABC=40°,求∠ADE 和∠AED 的度数;
(2)若 AB=30 cm,BD=18 cm,BC=20 cm,求 DE 的长.

答案:解:(1)因为△ABC∽△ADE
所以∠ADE=∠ABC= 40°,
∠AED=∠ACB= 180°- 75° - 40°=65°
(2)因为△ABC∽△ADE
所以$\frac {AB}{BD}=\frac {BC}{CE}$
因为$AB=30\ \mathrm {cm},$$BD=18\ \mathrm {cm},$$BC=20\ \mathrm {cm}$
所以$DE=8\ \mathrm {cm}.$
所以∠ADE=∠ABC= 40°,
∠AED=∠ACB= 180°- 75° - 40°=65°
(2)因为△ABC∽△ADE
所以$\frac {AB}{BD}=\frac {BC}{CE}$
因为$AB=30\ \mathrm {cm},$$BD=18\ \mathrm {cm},$$BC=20\ \mathrm {cm}$
所以$DE=8\ \mathrm {cm}.$
例 3 如图 6.3.3,四边形 ABCD 与四边形 A'B'C'D'相似,求相似比、CD 和 A'D'的长及α的大小.
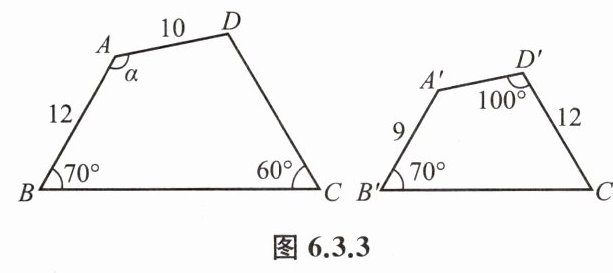

答案:例3 相似比为$\frac{4}{3}, A'D' = 7.5, CD = 16, α = 130°.$
解析:
解:因为四边形ABCD与四边形A'B'C'D'相似,所以对应角相等,对应边成比例。
在四边形ABCD中,∠B=70°,∠C=60°,在四边形A'B'C'D'中,∠B'=70°,∠D'=100°,所以∠B与∠B'是对应角,∠D与∠D'是对应角,故α=∠D=∠D'=100°。
AB=12,A'B'=9,所以相似比为AB:A'B'=12:9=4:3。
AD=10,设A'D'=x,因为AD:A'D'=4:3,所以10:x=4:3,解得x=7.5,即A'D'=7.5。
D'C'=12,设CD=y,因为CD:D'C'=4:3,所以y:12=4:3,解得y=16,即CD=16。
综上,相似比为$\frac{4}{3}$,A'D'=7.5,CD=16,α=100°。
在四边形ABCD中,∠B=70°,∠C=60°,在四边形A'B'C'D'中,∠B'=70°,∠D'=100°,所以∠B与∠B'是对应角,∠D与∠D'是对应角,故α=∠D=∠D'=100°。
AB=12,A'B'=9,所以相似比为AB:A'B'=12:9=4:3。
AD=10,设A'D'=x,因为AD:A'D'=4:3,所以10:x=4:3,解得x=7.5,即A'D'=7.5。
D'C'=12,设CD=y,因为CD:D'C'=4:3,所以y:12=4:3,解得y=16,即CD=16。
综上,相似比为$\frac{4}{3}$,A'D'=7.5,CD=16,α=100°。
1. 若△ABC∽△A'B'C',且$\frac{AB}{A'B'}=2$,则△ABC 与△A'B'C'的相似比是
2
,△A'B'C'与△ABC 的相似比是$\frac{1}{2}$
.答案:2
1:2
1:2
2. 若四边形 ABCD 与四边形 A'B'C'D'相似,且∠A=60°,∠B=115°,∠C'=87°,则∠D'=
98
°.答案:98
二、解答题
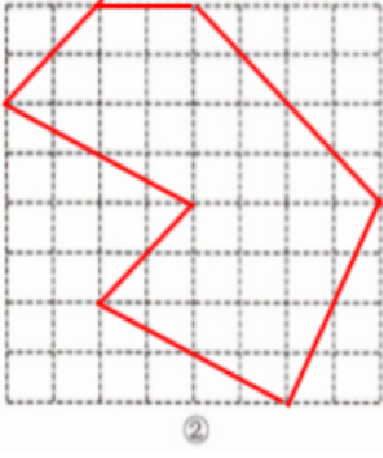
3. 在如图的网格中,将图①网格中的图形放大为原来的 2 倍,并画在图②网格中.
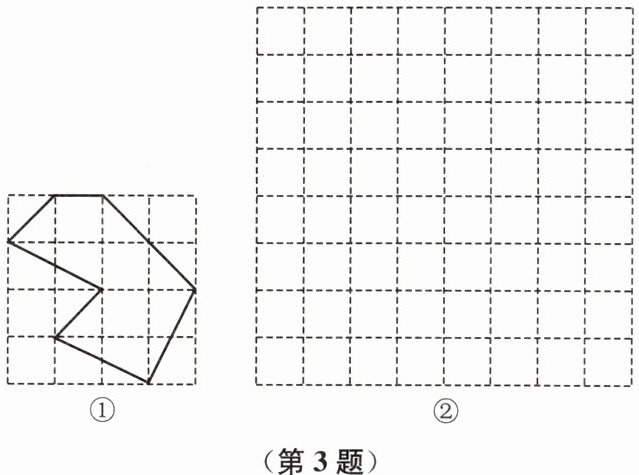
3. 在如图的网格中,将图①网格中的图形放大为原来的 2 倍,并画在图②网格中.

答案: