9. 如图,矩形$OABC$的顶点$A$在反比例函数$y=\frac{k}{x}(x<0)$的图像上,顶点$B$、$C$在第一象限内,对角线$AC // x$轴,交$y$轴于点$D$.若矩形$OABC$的面积是 6,$\cos \angle OAC=\frac{2}{3}$,求$k$的值.


答案:解:因为$cos∠OAC=\frac {2}{3}$
所以$cos∠OAC=\frac {AD}{AO}=\frac {AO}{AC}=\frac {2}{3}$
设AD=2a,则AO=3a
所以$AC=\frac {9}{2}a$
所以$\frac {AD}{AC}=\frac {2a}{\frac {9}{2}a}=\frac {4}{9}$
所以$2S_{△AOD}=\frac {4}{9}×2×S_{△AOC}=\frac {8}{9}×6=\frac {8}{3}$
因为k<0
所以$k=-\frac {8}{3}$
所以$cos∠OAC=\frac {AD}{AO}=\frac {AO}{AC}=\frac {2}{3}$
设AD=2a,则AO=3a
所以$AC=\frac {9}{2}a$
所以$\frac {AD}{AC}=\frac {2a}{\frac {9}{2}a}=\frac {4}{9}$
所以$2S_{△AOD}=\frac {4}{9}×2×S_{△AOC}=\frac {8}{9}×6=\frac {8}{3}$
因为k<0
所以$k=-\frac {8}{3}$
例 1 对于锐角 $\alpha$,若 $\tan \alpha = \frac{3}{4}$,求 $\sin \alpha$、$\cos \alpha$ 的值.
答案:
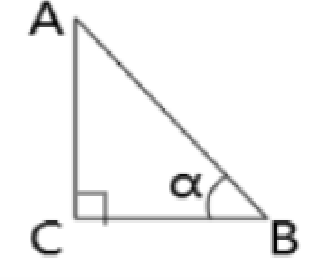
解:如图所示,∠B=a, ∠C=90°
设AC=3x
在Rt△ABC中
因为AC=3x,$tana=\frac {AC}{BC}=\frac {3}{4}$
所以BC=4x
所以$AB=\sqrt{AC²+BC²}= 5x$
$sina=\frac {AC}{AB}=\frac {3}{5}$
$cosa=\frac {BC}{AB}=\frac {4}{5}$
解:如图所示,∠B=a, ∠C=90°
设AC=3x
在Rt△ABC中
因为AC=3x,$tana=\frac {AC}{BC}=\frac {3}{4}$
所以BC=4x
所以$AB=\sqrt{AC²+BC²}= 5x$
$sina=\frac {AC}{AB}=\frac {3}{5}$
$cosa=\frac {BC}{AB}=\frac {4}{5}$

例 2 在透明纸上画一个 $45^{\circ}$ 角,记为 $\angle AOB$,将 $\angle AOB$ 剪下,摆放在一把刻度尺上(图 7.2.2),顶点 $O$ 与刻度尺下边缘的端点重合,$OA$ 与刻度尺下边缘重合,$OB$ 与刻度尺上边缘的交点 $B$ 在刻度尺上的读数为 $2\ \mathrm{cm}$. 若按相同的方式将 $37^{\circ}$ 的 $\angle AOC$ 放置在该刻度尺上,求 $OC$ 与刻度尺上边缘的交点 $C$ 在刻度尺上的读数.(精确到 $0.1\ \mathrm{cm}$;参考数据:$\sin 37^{\circ} \approx 0.60$,$\cos 37^{\circ} \approx 0.80$,$\tan 37^{\circ} \approx 0.75$)


答案:
解:过点B作BD⊥OA于D,
过点C作CE⊥OA于E.
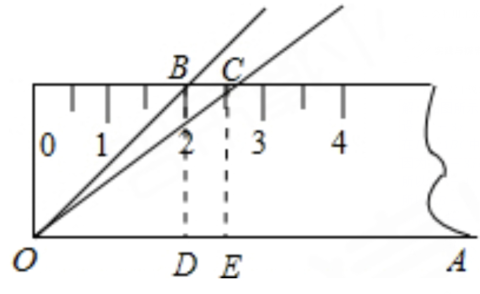
在△BOD中,∠BDO=90°,∠DOB=45°,
所以$BD=OD=2\ \mathrm {cm},$
所以$CE=BD=2\ \mathrm {cm}.$
在△COE中,∠CEO=90°, ∠COE=37°,
所以$tan_{37}°=\frac {CE}{OE}≈0.75,$
所以$OE≈2.7\ \mathrm {cm}.$
所以OC与尺上沿的交点C在尺上的读数约为$2.7\ \mathrm {cm}.$
解:过点B作BD⊥OA于D,
过点C作CE⊥OA于E.

在△BOD中,∠BDO=90°,∠DOB=45°,
所以$BD=OD=2\ \mathrm {cm},$
所以$CE=BD=2\ \mathrm {cm}.$
在△COE中,∠CEO=90°, ∠COE=37°,
所以$tan_{37}°=\frac {CE}{OE}≈0.75,$
所以$OE≈2.7\ \mathrm {cm}.$
所以OC与尺上沿的交点C在尺上的读数约为$2.7\ \mathrm {cm}.$