3. 在$\mathrm{Rt} \triangle ABC$中,$\angle C=90^{\circ}$,$AB=6$,$\cos B=\frac{2}{3}$,则$BC$的长为
4
.答案:解:在$\mathrm{Rt} \triangle ABC$中,$\cos B = \frac{BC}{AB}$(余弦的定义公式:$\cos B=\frac{邻边}{斜边}$,即$\cos B=\frac{BC}{AB}$)。
已知$AB = 6$,$\cos B=\frac{2}{3}$,将$AB = 6$,$\cos B=\frac{2}{3}$代入$\cos B = \frac{BC}{AB}$中,得到$\frac{2}{3}=\frac{BC}{6}$。
根据等式的性质,两边同时乘以$6$,可得$BC=\frac{2}{3}×6 = 4$。
所以$BC$的长为$4$。
已知$AB = 6$,$\cos B=\frac{2}{3}$,将$AB = 6$,$\cos B=\frac{2}{3}$代入$\cos B = \frac{BC}{AB}$中,得到$\frac{2}{3}=\frac{BC}{6}$。
根据等式的性质,两边同时乘以$6$,可得$BC=\frac{2}{3}×6 = 4$。
所以$BC$的长为$4$。
4. 比较大小:
(1) $\sin 28^{\circ}$_________$\sin 30^{\circ}$;(2) $\cos 44^{\circ}$_________$\cos 46^{\circ}$.
(1) $\sin 28^{\circ}$_________$\sin 30^{\circ}$;(2) $\cos 44^{\circ}$_________$\cos 46^{\circ}$.
答案:<
>
>
三、解答题
5. 如图,在$\mathrm{Rt} \triangle ABC$中,$AC=BC$,$\angle C=90^{\circ}$.求$\sin A$,$\cos B$的值.
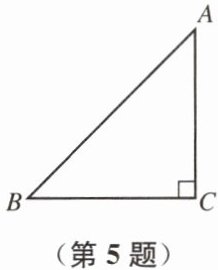
5. 如图,在$\mathrm{Rt} \triangle ABC$中,$AC=BC$,$\angle C=90^{\circ}$.求$\sin A$,$\cos B$的值.

答案:解:∵AC=BC,∠C=90°
∴$AB=\sqrt{AC^2+BC^2}=\sqrt{2}BC$
∴$sinA=\frac{BC}{AB}=\frac{BC}{\sqrt{2}BC}=\frac{\sqrt{2}}{2},$
$cosB=\frac{BC}{AB}=\frac{\sqrt{2}}{2}$
∴$AB=\sqrt{AC^2+BC^2}=\sqrt{2}BC$
∴$sinA=\frac{BC}{AB}=\frac{BC}{\sqrt{2}BC}=\frac{\sqrt{2}}{2},$
$cosB=\frac{BC}{AB}=\frac{\sqrt{2}}{2}$
6. 如图,在$\triangle ABC$中,$\angle C=90^{\circ}$,点$D$在$AC$上,$\angle DBC=\angle A$.若$AC=4$,$\cos A=\frac{4}{5}$,求$BD$的长.
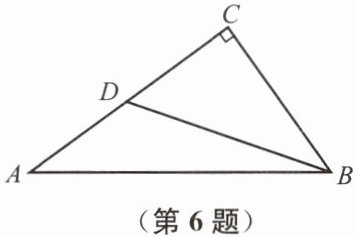

答案:解:$AB=\frac {AC}{cosA}=5$
$sinA=\frac {3}{5}$
BC=ABsinA=3
所以$BD=\frac {BC}{cos∠DBC}=\frac {3}{\frac {4}{5}}=\frac {15}{4}$
$sinA=\frac {3}{5}$
BC=ABsinA=3
所以$BD=\frac {BC}{cos∠DBC}=\frac {3}{\frac {4}{5}}=\frac {15}{4}$
7. 在$\triangle ABC$中,$\angle C=90^{\circ}$,$a$、$b$、$c$分别为$\angle A$、$\angle B$、$\angle C$的对边,若$b^{2}=ac$,求$\sin A$的值.
答案:$7. \frac{\sqrt{5}-1}{2}.$
解析:
在$\triangle ABC$中,$\angle C=90^{\circ}$,由勾股定理得$a^{2}+b^{2}=c^{2}$。
因为$b^{2}=ac$,所以$a^{2}+ac=c^{2}$。
等式两边同时除以$c^{2}$,得$\left(\frac{a}{c}\right)^{2}+\frac{a}{c}=1$。
设$\sin A=\frac{a}{c}=x$($0<x<1$),则方程化为$x^{2}+x - 1=0$。
解方程$x^{2}+x - 1=0$,判别式$\Delta=1^{2}-4×1×(-1)=5$,
所以$x=\frac{-1\pm\sqrt{5}}{2}$。
因为$0<x<1$,所以$x=\frac{-1+\sqrt{5}}{2}$,即$\sin A=\frac{\sqrt{5}-1}{2}$。
因为$b^{2}=ac$,所以$a^{2}+ac=c^{2}$。
等式两边同时除以$c^{2}$,得$\left(\frac{a}{c}\right)^{2}+\frac{a}{c}=1$。
设$\sin A=\frac{a}{c}=x$($0<x<1$),则方程化为$x^{2}+x - 1=0$。
解方程$x^{2}+x - 1=0$,判别式$\Delta=1^{2}-4×1×(-1)=5$,
所以$x=\frac{-1\pm\sqrt{5}}{2}$。
因为$0<x<1$,所以$x=\frac{-1+\sqrt{5}}{2}$,即$\sin A=\frac{\sqrt{5}-1}{2}$。
8. 在$□ ABCD$中,$\angle ABC$是锐角,将$CD$沿直线$l$翻折至$AB$所在直线,点$C$、$D$的对应点分别为$C^{\prime}$、$D^{\prime}$,若$AC^{\prime}:AB:BC=1:3:7$,则$\cos \angle ABC=$
$\frac{2}{7}$或$\frac{4}{7}$
.答案:$8. \frac{2}{7}$或$\frac{4}{7}.$
解析:
解:设$AC' = k$,$AB = 3k$,$BC = 7k$,四边形$ABCD$为平行四边形,$AB = CD = 3k$,$BC = AD = 7k$,$AB// CD$。
情况一:点$C'$在$AB$延长线上
由翻折性质,$C'D' = CD = 3k$,$D'C' = DC$,$AB// CD$,则$AD' = BC = 7k$。
在$\triangle ABC'$中,$AC' = k$,$AB = 3k$,$BC' = BC = 7k$。
由余弦定理:$AC'^2 = AB^2 + BC^2 - 2 · AB · BC · \cos\angle ABC$
即$k^2 = (3k)^2 + (7k)^2 - 2 · 3k · 7k · \cos\angle ABC$
解得$\cos\angle ABC = \frac{4}{7}$。
情况二:点$C'$在$BA$延长线上
此时$AC' = k$,$BC' = AB + AC' = 4k$。
在$\triangle ABC'$中,由余弦定理:$AC'^2 = AB^2 + BC^2 - 2 · AB · BC · \cos\angle ABC$
即$k^2 = (3k)^2 + (7k)^2 - 2 · 3k · 7k · \cos\angle ABC$
解得$\cos\angle ABC = \frac{2}{7}$。
综上,$\cos\angle ABC = \frac{2}{7}$或$\frac{4}{7}$。
$\frac{2}{7}$或$\frac{4}{7}$
情况一:点$C'$在$AB$延长线上
由翻折性质,$C'D' = CD = 3k$,$D'C' = DC$,$AB// CD$,则$AD' = BC = 7k$。
在$\triangle ABC'$中,$AC' = k$,$AB = 3k$,$BC' = BC = 7k$。
由余弦定理:$AC'^2 = AB^2 + BC^2 - 2 · AB · BC · \cos\angle ABC$
即$k^2 = (3k)^2 + (7k)^2 - 2 · 3k · 7k · \cos\angle ABC$
解得$\cos\angle ABC = \frac{4}{7}$。
情况二:点$C'$在$BA$延长线上
此时$AC' = k$,$BC' = AB + AC' = 4k$。
在$\triangle ABC'$中,由余弦定理:$AC'^2 = AB^2 + BC^2 - 2 · AB · BC · \cos\angle ABC$
即$k^2 = (3k)^2 + (7k)^2 - 2 · 3k · 7k · \cos\angle ABC$
解得$\cos\angle ABC = \frac{2}{7}$。
综上,$\cos\angle ABC = \frac{2}{7}$或$\frac{4}{7}$。
$\frac{2}{7}$或$\frac{4}{7}$