6. 若函数 $ y = a(x + h)^{2} + k $ 的图像可由函数 $ y = -\frac{1}{2}x^{2} $ 的图像先沿 $ x $ 轴向左平移 $ 2 $ 个单位长度,再沿 $ y $ 轴向上平移 $ 3 $ 个单位长度得到,则 $ a = $
$ -\frac{1}{2} $
,$ h = $$ 2 $
,$ k = $$ 3 $
.答案:$-\frac {1}{2}$
2
3
2
3
7. 若函数 $ y = 2x^{2} + bx + c $ 的顶点坐标是 $ (1, -2) $,则 $ b = $
$ -4 $
,$ c = $$ 0 $
.答案:-4
0
0
8. 函数 $ y = 2x^{2} + 3x + 3 $ 的图像的顶点坐标是
$ (-\frac{3}{4}, \frac{15}{8}) $
,对称轴是过点$(-\frac{3}{4}, \frac{15}{8})$且平行于$y$轴的直线
,它可由函数 $ y = 2x^{2} $ 的图像先沿$ x $轴向左平移$\frac{3}{4}$个单位长度
,再沿$ y $轴向上平移$\frac{15}{8}$个单位长度
得到.答案:$8.(- \frac{3}{4}, \frac{15}{8}) $过点$(- \frac{3}{4}, \frac{15}{8})$且平行于y轴的直线 x轴向左平移$\frac{3}{4}$个单位长度或y轴向上平移$\frac{15}{8}$个单位长度 y轴向上平移$\frac{15}{8}$个单位长度或x轴向左平移$\frac{3}{4}$个单位长度
9. 已知函数 $ y = \frac{1}{3}(x - 4)^{2} - 3 $ 的部分图像如图. 该图像与 $ x $ 轴的另一个交点的坐标是(

A.$ (5, 0) $
B.$ (6, 0) $
C.$ (7, 0) $
D.$ (8, 0) $
C
).
A.$ (5, 0) $
B.$ (6, 0) $
C.$ (7, 0) $
D.$ (8, 0) $
答案:C
10. 已知函数 $ y = -\frac{1}{4}x^{2} - 2x - 3 $.
- (1) 用配方法化成 $ y = a(x + h)^{2} + k $ 的形式.
- (2) 画出函数的图像并写出顶点坐标与对称轴.
- (3) 当 $ x $ 取何值时,$ y $ 有最大值或最小值?最大值或最小值是多少?
- (1) 用配方法化成 $ y = a(x + h)^{2} + k $ 的形式.
- (2) 画出函数的图像并写出顶点坐标与对称轴.
- (3) 当 $ x $ 取何值时,$ y $ 有最大值或最小值?最大值或最小值是多少?
答案:
解:$(1)y=-\frac 14(x^2+8x)-3=-\frac 14(x+4)^2+1$
(2)如图所示
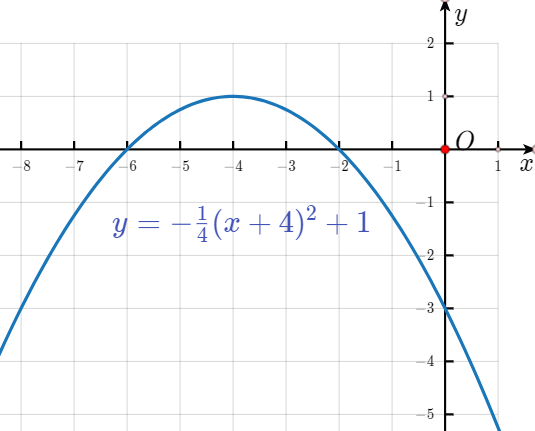
顶点坐标为(-4,1),对称轴为过点(-4,1)且平行于y轴的直线
(3)由图可知,当x=-4时,y取得最大值为1
解:$(1)y=-\frac 14(x^2+8x)-3=-\frac 14(x+4)^2+1$
(2)如图所示

顶点坐标为(-4,1),对称轴为过点(-4,1)且平行于y轴的直线
(3)由图可知,当x=-4时,y取得最大值为1
11. 将抛物线向右平移 $ 2 $ 个单位长度或向上平移 $ 1 $ 个单位长度,我们把这种变换称为抛物线的简单变换. 已知某抛物线经过两次简单变换后相应的函数表达式是 $ y = x^{2} + 1 $,则原抛物线相应的函数表达式不可能是(
A.$ y = x^{2} - 1 $
B.$ y = x^{2} + 6x + 5 $
C.$ y = x^{2} + 4x + 4 $
D.$ y = x^{2} + 8x + 17 $
B
).A.$ y = x^{2} - 1 $
B.$ y = x^{2} + 6x + 5 $
C.$ y = x^{2} + 4x + 4 $
D.$ y = x^{2} + 8x + 17 $
答案:B
12. 点 $ A(-4, y_{1}) $、$ B(-1, y_{2}) $ 在二次函数 $ y = \frac{1}{3}(x + 2)^{2} + 1 $ 的图像上,要比较 $ y_{1} $、$ y_{2} $ 的大小,只要把 $ A $、$ B $ 两点的横坐标分别代入这个函数表达式进行计算即可. 下面介绍另一种比较方法:在开口向上的二次函数图像上,到对称轴距离较大的点在到对称轴距离较小的点的上方,由此即可比较这两点纵坐标的大小. 如图,点 $ A $ 到对称轴的距离为 $ 2 $,点 $ B $ 到对称轴的距离为 $ 1 $,于是 $ y_{1} > y_{2} $.

试用上述方法解答下列问题:已知二次函数 $ y = a(x - 2)^{2} + c(a < 0) $,当自变量 $ x $ 分别取 $ \sqrt{2} $、$ 3 $、$ 0 $ 时,对应的函数值分别为 $ y_{1} $、$ y_{2} $、$ y_{3} $,则 $ y_{1} $、$ y_{2} $、$ y_{3} $ 的大小关系是

试用上述方法解答下列问题:已知二次函数 $ y = a(x - 2)^{2} + c(a < 0) $,当自变量 $ x $ 分别取 $ \sqrt{2} $、$ 3 $、$ 0 $ 时,对应的函数值分别为 $ y_{1} $、$ y_{2} $、$ y_{3} $,则 $ y_{1} $、$ y_{2} $、$ y_{3} $ 的大小关系是
$ y_3 < y_2 < y_1 $
.答案:$y_{3}<y_{2}<y_{1}$