20. (8分)如图,在$\triangle ABC$中,延长$BC$到点$D$,使$CD = BC$,取$AB$的中点$F$,连接$FD$交$AC$于点$E$.
(1)度量$AE$、$CE$,估计它们的比值;
(2)再画一个符合本题条件的图形,验证猜想,并予证明.

(1)度量$AE$、$CE$,估计它们的比值;
(2)再画一个符合本题条件的图形,验证猜想,并予证明.

答案:
解:(1)经测量$AE=1.5\ \mathrm {cm},$$CE=0.75\ \mathrm {cm}$
AE:CE=2:1
(2)作CH//AB交DF{于}H
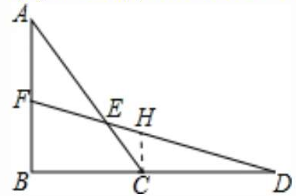
∵CH//AB,CD=BC
∴$\frac {CH}{BF}=\frac {1}{2}$
∵点F 是AB的中点
∴$\frac {CH}{AF}=\frac {1}{2}$
∵CH//AB
∴$\frac {AE}{CE}=\frac {AF}{CH}=2$
解:(1)经测量$AE=1.5\ \mathrm {cm},$$CE=0.75\ \mathrm {cm}$
AE:CE=2:1
(2)作CH//AB交DF{于}H

∵CH//AB,CD=BC
∴$\frac {CH}{BF}=\frac {1}{2}$
∵点F 是AB的中点
∴$\frac {CH}{AF}=\frac {1}{2}$
∵CH//AB
∴$\frac {AE}{CE}=\frac {AF}{CH}=2$
21. (9分)如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD⊥ AB$,垂足为$D$,$E$是$AC$的中点,$ED$、$CB$的延长线交于点$F$.
(1)求证:$\triangle FDB\backsim\triangle FCD$;
(2)如果$AC = 3$,$BC = 2$,求$\triangle CBD$、$\triangle FDB$的面积.

(1)求证:$\triangle FDB\backsim\triangle FCD$;
(2)如果$AC = 3$,$BC = 2$,求$\triangle CBD$、$\triangle FDB$的面积.

答案:证明:(1)∵CD⊥AB
$AB=\sqrt {AC^2+BC^2}=\sqrt {3^2+2^2}=\sqrt {13} $
∴$sin∠ABC=\frac {AC}{AB}=\frac {3\sqrt {13}}{13},$
$cos∠ABC=\frac {BC}{AB}=\frac {2\sqrt {13}}{13}$
在Rt△BCD中,
∵BC=2
∴$BD=BC · cos∠ABC=\frac {4\sqrt {13}}{13},$
$CD=BC · sin∠ABC=\frac {6\sqrt {13}}{13}$
∴$S_{△CBD}=\frac 12BD×CD=\frac {12}{13}$
设$S_{△FDB}=x$
∵△FDB∽△FCD
∴$\frac {S_{△FDB}}{S_{△FCD}}=(\frac {BD}{CD})^2=\frac 49$
∴$S_{△FCD}=\frac 94x$
∴$\frac 94x-x=\frac {12}{13}$
解得$x=\frac {48}{65}$
∴$S_{△FDB}=\frac {48}{65}$
∴∠ADC=∠BDC=90°
∵E为AC的中点
∴AE=DE
∴∠A=∠ADE
∵∠ADE=∠FDB
∴∠A=∠FDB
∵∠ADC=∠ACB=90°
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°
∴∠A=∠BCD=∠FDB
∵∠F=∠F
∴△FDB∽△FCD
(更多请点击查看作业精灵详解)
解:(2)在Rt△ACB中,由勾股定理得:$AB=\sqrt {AC^2+BC^2}=\sqrt {3^2+2^2}=\sqrt {13} $
∴$sin∠ABC=\frac {AC}{AB}=\frac {3\sqrt {13}}{13},$
$cos∠ABC=\frac {BC}{AB}=\frac {2\sqrt {13}}{13}$
在Rt△BCD中,
∵BC=2
∴$BD=BC · cos∠ABC=\frac {4\sqrt {13}}{13},$
$CD=BC · sin∠ABC=\frac {6\sqrt {13}}{13}$
∴$S_{△CBD}=\frac 12BD×CD=\frac {12}{13}$
设$S_{△FDB}=x$
∵△FDB∽△FCD
∴$\frac {S_{△FDB}}{S_{△FCD}}=(\frac {BD}{CD})^2=\frac 49$
∴$S_{△FCD}=\frac 94x$
∴$\frac 94x-x=\frac {12}{13}$
解得$x=\frac {48}{65}$
∴$S_{△FDB}=\frac {48}{65}$
22. (9分)如图,在$\triangle ABC$中,已知边$BC$的长为8,$BC$上的高为6,$\angle B$和$\angle C$都为锐角.解决下列问题:
在$AB$上任取一点,记为点$M$(不与点$A$、$B$重合),过点$M$作$MN// BC$,交$AC$于点$N$,画$\triangle AMN$关于直线$MN$对称的$\triangle A'MN$.若设$\triangle AMN$中边$MN$上的高为$x$,$\triangle A'MN$与四边形$BCNM$重叠部分的面积为$y$,用含$x$的代数式表示$y$.

在$AB$上任取一点,记为点$M$(不与点$A$、$B$重合),过点$M$作$MN// BC$,交$AC$于点$N$,画$\triangle AMN$关于直线$MN$对称的$\triangle A'MN$.若设$\triangle AMN$中边$MN$上的高为$x$,$\triangle A'MN$与四边形$BCNM$重叠部分的面积为$y$,用含$x$的代数式表示$y$.

答案:
解:
∵BC=8,BC上的高为6
∴△ABC的面积$=\frac {1}{2}×8×6=24$
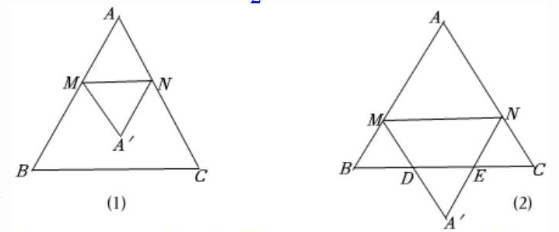
当0<x≤3时,如图(1),
△A'MN与四边形BCNM重叠部分的面积$y=S_{△AMN}$
∵MN//BC
∴△AMN∽△ABC
∴$\frac {y}{24}=(\frac {x}{6})^2$
∴$y=\frac {2}{3}x^2$
当3<x<6时,如图(2),重叠部分为梯形MDEN
∵DE//MN
∴△AMN∽△ABC
∴MN:BC=x:6
∴MN:8=x:6
∴$MN=\frac {4}{3}x$
∵△AMN≌△A'MN
∴△A'DE的边DE的高是2x-6
∵△A'DE∽△A'MN
∴DE:MN=(2x-6):x
∴DE:$\frac {4}{3}x=(2x-6)$:x
∴$DE=\frac {4}{3}(2x-6)$
∵梯形MNED的高是6-x
∴梯形MNED的面积$=\frac {1}{2}[\frac {4}{3}(2x-6)+\frac {4}{3}x](6-x)=-2x^2+16x-24$
∴$y=-2x^2+16x-24$
∴综上所述,$y=\begin{cases}{\dfrac {2}{3}x^2(0<x≤3)}\\{-2x^2+16x-24(3<x<6)}\end{cases}$
解:
∵BC=8,BC上的高为6
∴△ABC的面积$=\frac {1}{2}×8×6=24$

当0<x≤3时,如图(1),
△A'MN与四边形BCNM重叠部分的面积$y=S_{△AMN}$
∵MN//BC
∴△AMN∽△ABC
∴$\frac {y}{24}=(\frac {x}{6})^2$
∴$y=\frac {2}{3}x^2$
当3<x<6时,如图(2),重叠部分为梯形MDEN
∵DE//MN
∴△AMN∽△ABC
∴MN:BC=x:6
∴MN:8=x:6
∴$MN=\frac {4}{3}x$
∵△AMN≌△A'MN
∴△A'DE的边DE的高是2x-6
∵△A'DE∽△A'MN
∴DE:MN=(2x-6):x
∴DE:$\frac {4}{3}x=(2x-6)$:x
∴$DE=\frac {4}{3}(2x-6)$
∵梯形MNED的高是6-x
∴梯形MNED的面积$=\frac {1}{2}[\frac {4}{3}(2x-6)+\frac {4}{3}x](6-x)=-2x^2+16x-24$
∴$y=-2x^2+16x-24$
∴综上所述,$y=\begin{cases}{\dfrac {2}{3}x^2(0<x≤3)}\\{-2x^2+16x-24(3<x<6)}\end{cases}$