16. 图①、②中的两个等腰直角三角形全等,图①中的小正方形面积是9,则图②中的小正方形面积是(

A.12
B.8
C.9
D.10
B
).
A.12
B.8
C.9
D.10
答案:B
17. (6分)如图,在$\triangle ABC$和$\triangle ADE$中,$\angle BAD = \angle CAE$,$\angle ABC = \angle ADE$.
(1)写出图中两对相似三角形(不添加辅助线和字母);
(2)求证:$\angle ABE = \angle ACE$.

(1)写出图中两对相似三角形(不添加辅助线和字母);
(2)求证:$\angle ABE = \angle ACE$.

答案:解:(1)△ABC∽△ADE,△BAD∽△CAE
(2)证明:∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE
∵∠ABC=∠ADE
∴△ABC∽△ADE
∴$\frac {AB}{AC}=\frac {AD}{AE}$
∵∠BAD=∠CAE
∴△BAD∽△CAE
∴∠ABE=∠ACE
(2)证明:∵∠BAD=∠CAE
∴∠BAD+∠CAD=∠CAE+∠CAD,即∠BAC=∠DAE
∵∠ABC=∠ADE
∴△ABC∽△ADE
∴$\frac {AB}{AC}=\frac {AD}{AE}$
∵∠BAD=∠CAE
∴△BAD∽△CAE
∴∠ABE=∠ACE
18. (6分)如图,在矩形$ABCD$中,$AB = 4$,$BC = 6$,$M$是$BC$的中点,$DE⊥ AM$,垂足为$E$.
(1)求$\triangle ABM$的面积;
(2)求$DE$的长;
(3)求$\triangle ADE$的面积.

(1)求$\triangle ABM$的面积;
(2)求$DE$的长;
(3)求$\triangle ADE$的面积.

答案:解:$(1)$∵$BC=6,$点$M$是$BC$的中点
∴$BM=\frac 12BC=3$
∵$AB=4$
∴$S_{△ABM}=\frac 12×AB×BM=6$
解$:(2)$∵四边形$ABCD$是矩形$ $
∴$AD//BC,$$∠B=90°$
∴$∠DAE=∠AMB$
∵$DE⊥AM$
∴$∠DEA=∠B=90°$
∵$∠DAE=∠AMB,$$∠DEA=∠B$
∴$△ADE∽△AMB$
∴$\frac {DE}{DA}=\frac {AB}{AM}$
在$Rt△ABM$中,
∵$AB=4,$$BM=3$
∴$AM=\sqrt {AB^2+BM^2}=5$
∵$DA=BC=6$
∴$\frac {DE}{6}=\frac 45$
∴$DE=\frac {24}{5}$
解$:(3)$在$Rt△ADE$中,
∵$DA=6,$$DE=\frac {24}{5} $
∴$AE=\sqrt {DA^2-DE^2}=\frac {18}{5}$
∴$S_{△ADE}=\frac 12×AE×DE=\frac {216}{25}$
∴$BM=\frac 12BC=3$
∵$AB=4$
∴$S_{△ABM}=\frac 12×AB×BM=6$
解$:(2)$∵四边形$ABCD$是矩形$ $
∴$AD//BC,$$∠B=90°$
∴$∠DAE=∠AMB$
∵$DE⊥AM$
∴$∠DEA=∠B=90°$
∵$∠DAE=∠AMB,$$∠DEA=∠B$
∴$△ADE∽△AMB$
∴$\frac {DE}{DA}=\frac {AB}{AM}$
在$Rt△ABM$中,
∵$AB=4,$$BM=3$
∴$AM=\sqrt {AB^2+BM^2}=5$
∵$DA=BC=6$
∴$\frac {DE}{6}=\frac 45$
∴$DE=\frac {24}{5}$
解$:(3)$在$Rt△ADE$中,
∵$DA=6,$$DE=\frac {24}{5} $
∴$AE=\sqrt {DA^2-DE^2}=\frac {18}{5}$
∴$S_{△ADE}=\frac 12×AE×DE=\frac {216}{25}$
19. (8分)如图,在$\triangle ABC$中,点$D$在边$AC$上,且$CD = 2DA$,$\angle BAC = 45^{\circ}$,$\angle BDC = 60^{\circ}$,$CE⊥ BD$,垂足为$E$.
(1)图中的相等线段有:
(2)写出图中一对相似的三角形并证明.
(3)求$\triangle BEC$与$\triangle BEA$的面积之比.

(1)图中的相等线段有:
$DE=DA$,$EA=EB=EC$
.(2)写出图中一对相似的三角形并证明.
(3)求$\triangle BEC$与$\triangle BEA$的面积之比.

答案:
(1)DE=DA,EA=EB=EC
解: (2) △ADE∽△AEC,证明如下:
在Rt△CDE中,∵∠BDC=60°
∴∠DCE=30°
∴CD=2DE
∵CD=2DA
∴DE=DA
∴∠DEA=∠DAE
∵∠DEA+∠DAE=∠BDC= 60°
∴∠DEA=∠DAE=30°
∵∠DEA=∠ACE,∠DAE=∠CAE
∴△ADE∽△AEC
解:(3)过点A作AF⊥BD,交BD的延长线于点F,
如图所示
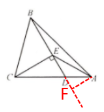
∵$S_{△BEC}$:$S_{△BEA}=\frac 12BE×CE$:$\frac 12BE×AF=CE$:AF
又
∵$S_{△CDE}$:$S_{△ADE}=\frac 12DE×CE$:$\frac 12DE×AF=CE$:AF
∴$S_{△BEC}$:$S_{△BEA}=S_{△CDE}$:$S_{△ADE}=CD$:DA
∵CD=2DA
∴$S_{△BEC}$:$S_{△BEA}=2$:1
(1)DE=DA,EA=EB=EC
解: (2) △ADE∽△AEC,证明如下:
在Rt△CDE中,∵∠BDC=60°
∴∠DCE=30°
∴CD=2DE
∵CD=2DA
∴DE=DA
∴∠DEA=∠DAE
∵∠DEA+∠DAE=∠BDC= 60°
∴∠DEA=∠DAE=30°
∵∠DEA=∠ACE,∠DAE=∠CAE
∴△ADE∽△AEC
解:(3)过点A作AF⊥BD,交BD的延长线于点F,
如图所示

∵$S_{△BEC}$:$S_{△BEA}=\frac 12BE×CE$:$\frac 12BE×AF=CE$:AF
又
∵$S_{△CDE}$:$S_{△ADE}=\frac 12DE×CE$:$\frac 12DE×AF=CE$:AF
∴$S_{△BEC}$:$S_{△BEA}=S_{△CDE}$:$S_{△ADE}=CD$:DA
∵CD=2DA
∴$S_{△BEC}$:$S_{△BEA}=2$:1