12. 阅读下面的材料,先完成阅读填空,再按要求答题:
$ \sin 30^{\circ} = \frac{1}{2} $, $ \cos 30^{\circ} = \frac{\sqrt{3}}{2} $,则 $ \sin^{2} 30^{\circ} + \cos^{2} 30^{\circ} = $_______; $ \sin 45^{\circ} = \frac{\sqrt{2}}{2} $, $ \cos 45^{\circ} = \frac{\sqrt{2}}{2} $,则 $ \sin^{2} 45^{\circ} + \cos^{2} 45^{\circ} = $_______; $ \sin 60^{\circ} = \frac{\sqrt{3}}{2} $, $ \cos 60^{\circ} = \frac{1}{2} $,则 $ \sin^{2} 60^{\circ} + \cos^{2} 60^{\circ} = $_______.
……
观察上述等式,猜想:对任意锐角 $ A $,都有 $ \sin^{2} A + \cos^{2} A = $_______.
(1) 如图,在锐角三角形 $ ABC $ 中,利用三角函数的定义及勾股定理证明你的猜想;
(2) 已知 $ \angle A $ 为锐角( $ \cos A > 0 $ ),且 $ \sin A = \frac{3}{5} $,求 $ \cos A $ 的值.

$ \sin 30^{\circ} = \frac{1}{2} $, $ \cos 30^{\circ} = \frac{\sqrt{3}}{2} $,则 $ \sin^{2} 30^{\circ} + \cos^{2} 30^{\circ} = $_______; $ \sin 45^{\circ} = \frac{\sqrt{2}}{2} $, $ \cos 45^{\circ} = \frac{\sqrt{2}}{2} $,则 $ \sin^{2} 45^{\circ} + \cos^{2} 45^{\circ} = $_______; $ \sin 60^{\circ} = \frac{\sqrt{3}}{2} $, $ \cos 60^{\circ} = \frac{1}{2} $,则 $ \sin^{2} 60^{\circ} + \cos^{2} 60^{\circ} = $_______.
……
观察上述等式,猜想:对任意锐角 $ A $,都有 $ \sin^{2} A + \cos^{2} A = $_______.
(1) 如图,在锐角三角形 $ ABC $ 中,利用三角函数的定义及勾股定理证明你的猜想;
(2) 已知 $ \angle A $ 为锐角( $ \cos A > 0 $ ),且 $ \sin A = \frac{3}{5} $,求 $ \cos A $ 的值.

答案:
1 1 1 1
解:(1)过点B作BD⊥AC,垂足为点D
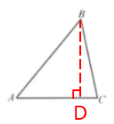
在Rt△ABD中,由勾股定理可得,$AB^2=AD^2+BD^2$
∵$sinA=\frac {BD}{AB},$$cosA=\frac {AD}{AB}$
∴$sin^2A+cos^2A=\frac {BD^2+AD^2}{AB^2}=1$
(2)
∵$sinA=\frac 35,$$sin^2A+cos^2A=1$
∴$cos^2A=1-sin^2A=\frac {16}{25}$
∵∠A为锐角(cosA>0)
∴$cosA=\sqrt {\frac {16}{25}}=\frac 45$
1 1 1 1
解:(1)过点B作BD⊥AC,垂足为点D

在Rt△ABD中,由勾股定理可得,$AB^2=AD^2+BD^2$
∵$sinA=\frac {BD}{AB},$$cosA=\frac {AD}{AB}$
∴$sin^2A+cos^2A=\frac {BD^2+AD^2}{AB^2}=1$
(2)
∵$sinA=\frac 35,$$sin^2A+cos^2A=1$
∴$cos^2A=1-sin^2A=\frac {16}{25}$
∵∠A为锐角(cosA>0)
∴$cosA=\sqrt {\frac {16}{25}}=\frac 45$
13. 如图,在 $ \triangle ABC $ 中, $ \angle C = 90^{\circ} $, $ D $ 是 $ BC $ 上的一点, $ \angle ADC = 45^{\circ} $, $ BD = 2DC $. 求 $ \cos B $ 和 $ \sin \angle BAD $ 的值.


答案:
解:过点B作BE⊥AD,交AD的延长线于点E
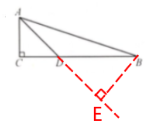
设DC=x,则BD=2x,BC=BD+DC=3x
∵∠ADC=45°,∠C=90°
∴△ACD是等腰直角三角形
∴AC=DC=x
在Rt△BCD中,∵BC=3x,AC=x
∴$AB=\sqrt {BC^2+AC^2}=\sqrt {10}x$
∴$cosB=\frac {BC}{AB}=\frac {3x}{\sqrt {10}x}=\frac {3\sqrt {10}}{10}$
∵∠BDE=∠ADC=45°,BE⊥AD
∴△BDE是等腰直角三角形
∵BD=2x
∴$BE=DE=\frac {BD}{\sqrt 2}=\sqrt 2x$
∵△ACD是等腰直角三角形,CD=x
∴$AD=\sqrt 2CD=\sqrt 2x$
∴$AE=AD+DE=2\sqrt 2x$
在Rt△ABE中,∵$AE=2\sqrt 2x,$$BE=\sqrt 2x$
∴$AB=\sqrt {AE^2+BE^2}=\sqrt {10}x$
∴$sin∠BAD=\frac {BE}{AB}=\frac {\sqrt 2x}{\sqrt {10}x}=\frac {\sqrt 5}5$
综上所述,$cosB=\frac {3\sqrt {10}}{10},$$sin∠BAD=\frac {\sqrt 5}5$
解:过点B作BE⊥AD,交AD的延长线于点E

设DC=x,则BD=2x,BC=BD+DC=3x
∵∠ADC=45°,∠C=90°
∴△ACD是等腰直角三角形
∴AC=DC=x
在Rt△BCD中,∵BC=3x,AC=x
∴$AB=\sqrt {BC^2+AC^2}=\sqrt {10}x$
∴$cosB=\frac {BC}{AB}=\frac {3x}{\sqrt {10}x}=\frac {3\sqrt {10}}{10}$
∵∠BDE=∠ADC=45°,BE⊥AD
∴△BDE是等腰直角三角形
∵BD=2x
∴$BE=DE=\frac {BD}{\sqrt 2}=\sqrt 2x$
∵△ACD是等腰直角三角形,CD=x
∴$AD=\sqrt 2CD=\sqrt 2x$
∴$AE=AD+DE=2\sqrt 2x$
在Rt△ABE中,∵$AE=2\sqrt 2x,$$BE=\sqrt 2x$
∴$AB=\sqrt {AE^2+BE^2}=\sqrt {10}x$
∴$sin∠BAD=\frac {BE}{AB}=\frac {\sqrt 2x}{\sqrt {10}x}=\frac {\sqrt 5}5$
综上所述,$cosB=\frac {3\sqrt {10}}{10},$$sin∠BAD=\frac {\sqrt 5}5$