7. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle A = 60^{\circ}$,$a + b = \sqrt{3} + 1$,解这个直角三角形.
答案:解:在Rt△ABC中,∵∠A=60°
∴∠B=90°-60°=30°,$tanA=\frac a{b}=\sqrt 3$
∴$a=\sqrt 3b$
∵$a+b=\sqrt 3b+b=\sqrt 3+1$
∴b=1,$a=\sqrt 3$
∴$c=\sqrt {a^2+b^2}=2$
∴∠B=90°-60°=30°,$tanA=\frac a{b}=\sqrt 3$
∴$a=\sqrt 3b$
∵$a+b=\sqrt 3b+b=\sqrt 3+1$
∴b=1,$a=\sqrt 3$
∴$c=\sqrt {a^2+b^2}=2$
8. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$BC = 4$,$AB = 4\sqrt{2}$,则$AC =$
$4$
,$\angle A =$$45^{\circ}$
,$\angle B =$$45^{\circ}$
.答案:4
45°
45°
45°
45°
9. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 9$,$\sin B = \frac{3}{5}$,则$AB$等于(
A.15
B.12
C.9
D.6
A
).A.15
B.12
C.9
D.6
答案:A
10. 已知$\angle A$是锐角,$\sin A = \frac{3}{5}$,则$5\cos A =$(
A.4
B.3
C.$\frac{15}{4}$
D.5
A
).A.4
B.3
C.$\frac{15}{4}$
D.5
答案:A
11. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$a$、$b$、$c$分别是$\angle A$、$\angle B$、$\angle C$的对边. 根据已知条件解直角三角形:
(1) $c = 8\sqrt{3}$,$\angle A = 60^{\circ}$;
(2) $a = 3\sqrt{6}$,$\angle A = 30^{\circ}$;
(3) $a = 6$,$b = 2\sqrt{3}$.
(1) $c = 8\sqrt{3}$,$\angle A = 60^{\circ}$;
(2) $a = 3\sqrt{6}$,$\angle A = 30^{\circ}$;
(3) $a = 6$,$b = 2\sqrt{3}$.
答案:解:(1)∠B=90°-∠A=30°
∴$a=csinA=8\sqrt 3×\frac {\sqrt 3}2=12,$$b=ccosA=8\sqrt 3×\frac 12=4\sqrt 3$
(2)∠B=90°-∠A=60°
$c=\frac {a}{sinA}=\frac {3\sqrt 6}{\frac 12}=6\sqrt 6,$$b=\frac a{tanA}=\frac {3\sqrt 6}{\frac {\sqrt 3}3}=9\sqrt 2$
$(3)c=\sqrt {a^2+b^2}=4\sqrt 3$
$sinB=\frac b{c}=\frac {2\sqrt 3}{4\sqrt 3}=\frac 12$
∴∠B=30°,∠A=90°-∠B=60°
∴$a=csinA=8\sqrt 3×\frac {\sqrt 3}2=12,$$b=ccosA=8\sqrt 3×\frac 12=4\sqrt 3$
(2)∠B=90°-∠A=60°
$c=\frac {a}{sinA}=\frac {3\sqrt 6}{\frac 12}=6\sqrt 6,$$b=\frac a{tanA}=\frac {3\sqrt 6}{\frac {\sqrt 3}3}=9\sqrt 2$
$(3)c=\sqrt {a^2+b^2}=4\sqrt 3$
$sinB=\frac b{c}=\frac {2\sqrt 3}{4\sqrt 3}=\frac 12$
∴∠B=30°,∠A=90°-∠B=60°
12. 在$\triangle ABC$中,$\angle C = 90^{\circ}$,$\angle A = 30^{\circ}$,角平分线$BD$的长为$8\ cm$. 求这个三角形的$3$条边的长.
答案:解:由已知可得△BCD是含30°的直角三角形
∴$CD=\frac {1}{2}\ \mathrm {BD}=\frac {1}{2} ×8=4\ \mathrm {cm}$
△ADB是等腰三角形,∴$AD=BD=8\ \mathrm {cm}$
则有$AC=8+4=12\ \mathrm {cm},$$BC=AC ·tan 30°=12× \frac {\sqrt{3}}{3}=4 \sqrt{3}\ \mathrm {cm}$
$AB=\sqrt{(4\sqrt{3})^2+12^2}=\sqrt{48+144}=\sqrt{192}=8 \sqrt{3}\ \mathrm {cm}$
∴$CD=\frac {1}{2}\ \mathrm {BD}=\frac {1}{2} ×8=4\ \mathrm {cm}$
△ADB是等腰三角形,∴$AD=BD=8\ \mathrm {cm}$
则有$AC=8+4=12\ \mathrm {cm},$$BC=AC ·tan 30°=12× \frac {\sqrt{3}}{3}=4 \sqrt{3}\ \mathrm {cm}$
$AB=\sqrt{(4\sqrt{3})^2+12^2}=\sqrt{48+144}=\sqrt{192}=8 \sqrt{3}\ \mathrm {cm}$
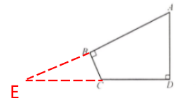
13. 如图,在四边形$ABCD$中,$AD = CD$,$AB = 5$,$\angle B = \angle D = 90^{\circ}$,$\tan A = 2$. 求$BC$的长.


答案:
解:延长AB、DC交于点E
∵∠B=∠D=90°
∴∠A+∠BCD=180°
∵∠BCE+∠BCD=180°
∴∠A=∠BCE
∴tanA=tan∠BCE=2
设BC=x,则BE=2x
在Rt△BCE中,∵BC=x,BE=2x
∴$CE=\sqrt {BC^2+BE^2}=\sqrt 5x$
∵$tanA=\frac {DE}{AD}=2$
∴AD:DE:AE=1:2:$\sqrt 5$
∵DE=2AD,AD=CD
∴$CE=CD=AD=\sqrt 5x$
∵AB=5,BE=2x
∴AE=2x+5
∵$AE=\sqrt 5AD$
∴$2x+5=\sqrt 5 · \sqrt 5x$
解得$x=\frac 53$
∴BC的长为$\frac 53$
解:延长AB、DC交于点E

∵∠B=∠D=90°
∴∠A+∠BCD=180°
∵∠BCE+∠BCD=180°
∴∠A=∠BCE
∴tanA=tan∠BCE=2
设BC=x,则BE=2x
在Rt△BCE中,∵BC=x,BE=2x
∴$CE=\sqrt {BC^2+BE^2}=\sqrt 5x$
∵$tanA=\frac {DE}{AD}=2$
∴AD:DE:AE=1:2:$\sqrt 5$
∵DE=2AD,AD=CD
∴$CE=CD=AD=\sqrt 5x$
∵AB=5,BE=2x
∴AE=2x+5
∵$AE=\sqrt 5AD$
∴$2x+5=\sqrt 5 · \sqrt 5x$
解得$x=\frac 53$
∴BC的长为$\frac 53$