6. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,点$D$在$BC$上,且$BD = 100$,$\angle ADC = 60^{\circ}$,$\sin B = \frac{\sqrt{2}}{2}$. 求$AC$的长(精确到$0.1$).


答案:解:∵$sinB=\frac {\sqrt 2}2$
∴∠B=∠BAC=45°
∴BC=AC
设BC=AC=x,则DC=x-100
在Rt△ACD中,∵∠ADC=60°
∴$tan ∠ADC=\frac {AC}{DC}=\sqrt 3$
∴$\frac x{x-100}=\sqrt 3$
解得$x=150+50\sqrt 3≈236.6$
∴AC的长为236.6
∴∠B=∠BAC=45°
∴BC=AC
设BC=AC=x,则DC=x-100
在Rt△ACD中,∵∠ADC=60°
∴$tan ∠ADC=\frac {AC}{DC}=\sqrt 3$
∴$\frac x{x-100}=\sqrt 3$
解得$x=150+50\sqrt 3≈236.6$
∴AC的长为236.6
7. 在$\triangle ABC$中,$\angle C = 90^{\circ}$. 若$b = \sqrt{2}$,$c = 2$,则$a =$
$\sqrt{2}$
,$\angle A =$$45^{\circ}$
.答案:$\sqrt{2}$
45°
45°
8. 在$\triangle ABC$中,$\angle C = 90^{\circ}$. 若$AC = 3$,$BC = 4$,则$\sin B =$
$\frac{3}{5}$
.答案:$\frac {3}{5}$
9. 在$\triangle ABC$中,$\angle C = 90^{\circ}$. 若$c = 7$,$\angle A = 30^{\circ}$,则$b =$
$\frac{7\sqrt{3}}{2}$
,$a =$$3\frac{1}{2}$
.答案:$\frac {7\sqrt{3}}{2} $
$3\frac {1}{2}$
$3\frac {1}{2}$
10. 如图是一个中心对称图形,$A$为对称中心. 若$\angle C = 90^{\circ}$,$\angle B = 30^{\circ}$,$BC = 1$,则$BB' =$(

A.$4$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{2\sqrt{3}}{3}$
D.$\frac{4\sqrt{3}}{3}$
D
).
A.$4$
B.$\frac{\sqrt{3}}{3}$
C.$\frac{2\sqrt{3}}{3}$
D.$\frac{4\sqrt{3}}{3}$
答案:D
11. 如图,在$\mathrm{Rt} \triangle ABC$中,斜边$AB = m$,$\angle B = 40^{\circ}$,则$BC$等于(

A.$m \sin 40^{\circ}$
B.$m \cos 40^{\circ}$
C.$m \tan 40^{\circ}$
D.$\frac{m}{\tan 40^{\circ}}$
B
).
A.$m \sin 40^{\circ}$
B.$m \cos 40^{\circ}$
C.$m \tan 40^{\circ}$
D.$\frac{m}{\tan 40^{\circ}}$
答案:B
12. 等腰三角形的周长为$5(2 + \sqrt{3})$,顶角是底角的$4$倍,求各角与各边的长.
答案:
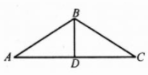
解:∵如图,设底角为a,则顶角为4a
∴6a=180°
∴a=30°,4a=120°
过点B作BD⊥AC,垂足为D,并设BD=x,则$ AD=\sqrt 3x$
∴$4x+2 \sqrt{3} x=5(2+ \sqrt{3} )$
∴$x=\frac {5}{2},$$AB=BC=2× \frac {5}{2}=5,$$AC=2 \sqrt{3} × \frac {5}{2}=5 \sqrt{3}$
解:∵如图,设底角为a,则顶角为4a
∴6a=180°
∴a=30°,4a=120°
过点B作BD⊥AC,垂足为D,并设BD=x,则$ AD=\sqrt 3x$
∴$4x+2 \sqrt{3} x=5(2+ \sqrt{3} )$
∴$x=\frac {5}{2},$$AB=BC=2× \frac {5}{2}=5,$$AC=2 \sqrt{3} × \frac {5}{2}=5 \sqrt{3}$
